El concepto de “asistencia gravitatoria” ha resultado ser fundamental para facilitar la exploración de nuestro “patio trasero”, el sistema solar. Esta técnica también ha sido utilizada para rescatar un satélite de comunicaciones en órbita alrededor de la Tierra cuyo vehículo lanzador no había conseguido inyectarlo en la órbita deseada.

Un poco de historia:

Varias naves no tripuladas se han aprovechado de la estrategia de “asistencias gravitatorias” para alcanzar sus objetivos de exploración en áreas distantes del sistema solar. Por ejemplo, la sonda Voyager 2 fue lanzada en agosto de 1977 y sobrevoló Júpiter empleando una “asistencia gravitatoria” para conseguir un impulso en su trayectoria hacia Saturno. La Voyager 1 fue lanzada el mes siguiente y realizó la misma maniobra (llegando a Júpiter antes que Voyager 2). La Voyager 2 obtuvo entonces una asistencia de Saturno y una más tarde de Urano, llegando de esa forma a Neptuno y más allá. Galileo usó asistencias gravitatorias para ganar energía, una en Venus y dos en la Tierra, mientras orbitaba el Sol en su trayectoria hacia Júpiter, su destino final. La nave Cassini-Huygens recibió dos asistencias de Venus, una de la Tierra, y otra de Júpiter para conseguir suficiente cantidad de movimiento para llegar a Saturno.

La estrategia de sobrevuelo con asistencia gravitatoria puede añadir o sustraer cantidad de movimiento para aumentar o disminuir la energía de la órbita de una nave. Normalmente se ha usado en órbitas alrededor del Sol, para aumentar la velocidad de la nave y propulsarla hacia el exterior del sistema solar, más lejos del Sol de lo que su vehículo lanzador hubiera sido capaz de lograr. Un sobrevuelo puede también disminuir el momento angular orbital de una nave, como en el caso de Galileo, donde se usó una “asistencia gravitatoria” por delante de la luna más grande de Júpiter, Io. De esta forma se consiguió que Galileo disminuyera su energía y se redujo la masa de propulsante del motor cohete necesaria para la inserción en la órbita de Júpiter. Los cometas y otros cuerpos en órbita alrededor del Sol experimentan de forma natural cambios en su órbita cuando pasan cerca de un planeta o luna.

Las dos naves Voyager son un ejemplo clásico de cómo usar las asistencias gravitatorias para alcanzar sus destinos. Se lanzaron a bordo de un Titan-III/Centaur, con destino a Saturno y más allá. Pero sus vehículos lanzadores podían proporcionarles suficiente energía para llegar tan sólo a Júpiter (a mitad de camino hacia Saturno). Si Júpiter no hubiese intervenido, y las dos naves no se hubiesen encontrado con el planeta gigante gaseoso, habrían permanecido en una órbita alrededor del Sol indefinidamente, alcanzando una distancia máxima del Sol (denominada afelio) igual al radio orbital de Júpiter (5 UA o 750 000 000 Km). En la parte opuesta de la órbita, la nave estaría en el punto más cercano al Sol (denominado perihelio) a la distancia de la órbita de la Tierra (1 UA o 150 000 000 Km).

Los dos momentos de lanzamiento para las naves Voyager se calcularon para que Júpiter pasara cerca en el momento adecuado. Debido a esto sintieron los efectos del tirón gravitacional de Júpiter y empezaron a ser atraídas hacia él. Afortunadamente sus velocidades fueron controladas al elegir con cuidado lo cerca que pasarían de Júpiter sin chocar con el planeta. Mientras las dos naves se escapaban de Júpiter, disminuyeron de nuevo su velocidad respecto al gigante gaseoso, llegando al final a la misma velocidad que tenían al entrar.

Cómo funciona

Desde el punto de vista de Júpiter, la situación es similar a la de un ciclista que acelera al bajar una cuesta hacia un valle y luego decelera en el tramo cuesta arriba del camino.

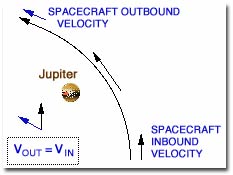
Figura 1, Asistencia Gravitatoria

En el diagrama de la derecha, la situación se explica en dos dimensiones. Puede observarse el módulo y la dirección de la velocidad de la nave a la llegada a Júpiter en la esquina inferior derecha de la figura. En la esquina superior izquierda, la fuerza gravitacional de Júpiter ha causado un cambio importante en la dirección de la velocidad de la nave, pero no en el módulo. (Ambas representan la velocidad en el “infinito”, respecto a Júpiter, es decir, antes y después de que se noten cambios debido a la presencia de Júpiter). A la mitad del diagrama, la flecha alargada muestra que hay un incremento importante, pero sólo por un tiempo, en el módulo de la velocidad.

Para comparar el fenómeno con el caso del ciclista, “V-in” (velocidad de entrada) muestra al ciclista acercándose cuesta abajo hacia el valle. “V-out” (velocidad de salida) muestra al ciclista disminuyendo de velocidad mientras sube la cuesta de salida. De hecho, después de pasar el valle, la dirección del ciclista ha cambiado, pero al final no ha aumentado o disminuido la velocidad de la bicicleta.

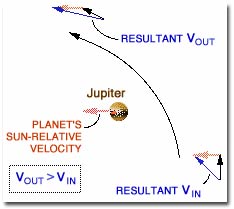
Figura 2, Asistencia Gravitatoria

El movimiento del planeta es una de las claves. Una asistencia gravitatoria de Júpiter no conlleva un planeta estacionario como se muestra arriba, sino un planeta con un enorme momento angular orbitando alrededor del Sol. En el diagrama de la izquierda, el movimiento de Júpiter alrededor del Sol se ha representado con un vector de color rojo. La nave aumenta su velocidad del orden de ese vector, o una parte importante de éste, durante su interacción con Júpiter. El vector rojo se suma a “V-in” y “V-out”. El resultado muestra que la velocidad del satélite, con respecto al Sol, se ve incrementada considerablemente gracias a Júpiter.

La otra clave es un concepto denominado “curvatura de la trayectoria”. Se puede observar cómo la rotación del vector velocidad de “V-in” a “V-out” (la curvatura de la trayectoria de la nave por la gravedad del planeta) ayuda a que aumente el resultado. La nave es una masa física, por lo que tiene su propia gravedad. Así es como la nave puede también atraer a Júpiter y disminuir el momento angular orbital de planeta en una cantidad muy pequeña. A cambio, la nave obtiene una cantidad de momento angular bastante importante comparada con el momento que ya tenía.

En la analogía de tirar una pelota de ping-pong a un ventilador eléctrico, la bola tomaría energía de la pala del ventilador y podemos suponer que rebotará a una velocidad mayor que la que tenía al llegar. En este caso, la pelota interacciona con la pala del ventilador directamente, en vez de gravitacionalmente, y disminuye ligeramente la velocidad del ventilador al golpearle. (Si el motor del ventilador estuviese encendido, el momento perdido por la pala sería reemplazado inmediatamente, lo que no ocurre en el caso de un planeta en órbita).

El mito de la honda

A menudo se ha comparado una asistencia gravitatoria con los efectos de una honda. Pero en realidad, las asistencias gravitatorias son, en términos físicos, un ejemplo completamente diferente. Al usar una honda, una persona haría girar el proyectil unas cuantas veces, cada vez más fuerte y apuntando mejor, antes de soltarlo. En ese momento, la fuerza centrífuga del proyectil se convierte en su fuerza propulsiva. Sin embargo, en las asistencias gravitatorias, una nave roba un poco de momento angular durante un solo sobrevuelo del planeta en movimiento, disminuyendo el momento del planeta. Una asistencia gravitatoria se parece mucho más a una pelota de ping-pong que golpea una de las palas giratorias de un ventilador de techo que a una honda.