Los Sulbasutras de la India

El pueblo Védico entró en la India alrededor del año 1500 a.C. desde la región del actual Irán. El término Védico hace referencia a la religión de estos pueblos y viene de la colección de sus textos sagrados conocidos como los Vedas. Los textos datan de entre los siglos XV a V a.C. y se usaban para los rituales de sacrificio que eran la principal característica de esta religión. Existía un ritual que se realizaba sobre un altar en el que se ofrecía en sacrificio comida, aunque algunas veces sacrificaban animales.

Los Vedas contienen cánticos y recitaciones destinadas a usarse en estas ceremonias. Posteriormente se añadió la prosa llamada Brahmanas, que explicaban cómo debían usarse los textos en las ceremonias. También relataban el origen y la importancia de los ritos propiamente dichos. Los Sulbasutras son apéndices de los Vedas en los que se dan normas para la construcción de altares. Para que el sacrificio ritual tuviera éxito, el altar tenía que ajustarse a medidas muy precisas.

La gente hacía sacrificios a sus dioses para que estuvieran contentos y le diesen abundante comida, buena suerte, salud, una vida larga y muchos otros beneficios materiales. Para tener contentos a los dioses todo se tenía que realizar siguiendo una fórmula muy precisa, por lo que la exactitud matemática se veía como algo de importancia capital. También deberíamos tener en cuenta que existían dos clases de rituales de sacrificio. Uno era una gran reunión pública mientras que el otro era un asunto familiar de menor importancia. Se necesitaban diferentes tipos de altar para los diferentes tipos de ceremonia. Todo lo que se sabe de las matemáticas védicas se halla en los Sulbasutras. Esto nos plantea un problema, ya que no sabemos si estos pueblos emprendieron sus investigaciones matemáticas por motivos propios, tal como hicieron los antiguos griegos, o si sólo lo hicieron para resolver los problemas necesarios para sus ritos religiosos. Ciertos historiadores han argumentado que las matemáticas, en particular la geometría, también debieron existir para apoyar los trabajos de astronomía que se realizaban por aquella época.

Es cierto que los Sulbasutras no contienen ninguna demostración de las reglas que describen. Algunas de esas reglas, como el método para construir un cuadrado de área igual a un rectángulo dado, son exactas. Otras, como la construcción de un cuadrado de área igual a un círculo dado, son aproximaciones. Veremos ambos ejemplos más abajo pero lo que queremos resaltar aquí es que los Sulbasutras no hacen distinción entre los dos. ¿Sabían los redactores de los Sulbasutras qué métodos eran exactos y cuáles aproximaciones? Los Sulbasutras fueron escritos por un escriba, aunque no era el tipo de escriba que simplemente hace una copia de un documento existente, si no del que añade bastante contenido. Todos los resultados matemáticos podrían deberse a estos escribas. No sabemos nada de los hombres que escribieron los Sulbasutras salvo sus nombres y una indicación aproximada del período en el que vivieron. Como de muchos matemáticos antiguos, nuestro único conocimiento de ellos son sus escritos. De estos documentos, el más importante es el Sulbasutra de Baudhayana y el Sulbasutra de Apastamba, escritos sobre los años 800 a.C. y 600 a.C. respectivamente. Los historiadores de las matemáticas también han estudiado y escrito sobre otros Sulbasutras de menor importancia, como el Sulbasutra de Manava o el de Katyayana escritos alrededor de los años 750 a.C. y 200 a.C. respectivamente. Examinemos ahora algo de las matemáticas que contienen los Sulbasutras. El primer resultado que era claramente conocido por los autores era el teorema de Pitágoras. El Sulbasutra de Baudhayana sólo nos da un caso especial del teorema de forma explícita:

La soga que se tiende a lo largo de la diagonal de un cuadrado produce un área que es el doble de la del cuadrado original

El Sulbasutra de Katyayana, sin embargo, da una versión más general:

La soga que se tiende sobre la diagonal de un rectángulo produce un área que es la que dan los lados vertical y horizontal juntos

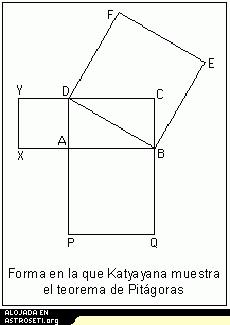En la figura de la derecha se ilustra este resultado. Observemos que los resultados se plantean en términos de ‘sogas’. De hecho, aunque Sulbasutra significaba originalmente normas que rigen los ritos religiosos, sutras viene a significar soga para medir un altar. Mientras pensamos en las declaraciones explícitas del teorema de Pitágoras, conviene darse cuenta de que hay muchos ejemplos de ternas pitagóricas en los Sulbasutras, dado que se usan frecuentemente. Como ejemplos podemos hallar

(5, 12, 13), (12, 16, 20), (8, 15, 17), (15, 20, 25), (12, 35, 37), (15, 36, 39), (⁵/₂, 6, ¹³/₂) y (¹⁵/₂, 10, ²⁵/₂).

Los Sulbasutras son en realidad manuales para la construcción de formas geométricas como cuadrados, círculos, rectángulos, etc. y podemos ilustrarlo con varios ejemplos.

La primera construcción que examinamos se da en la mayoría de los Sulbasutras. Es una construcción, basada en el teorema de Pitágoras, para hacer un cuadrado igual en área a dos cuadrados diferentes dados.

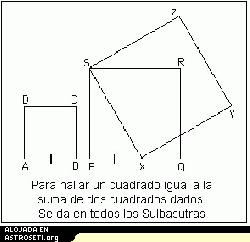Considere el diagrama de la izquierda: ABCD y PQRS son dos cuadrados dados. Marcar el punto X sobre PQ de manera que PX sea igual a AB. Entonces el cuadrado sobre SX tiene un área igual a la suma de las áreas de ABCD y PQRS. Esto es consecuencia del teorema de Pitágoras ya que SX² = PX² + PS². La siguiente construcción que examinamos es aquella en la que hallamos un cuadrado de área igual a la de un rectángulo dado. Damos la versión tal como aparece en el Sulbasutra de Baudhayana.

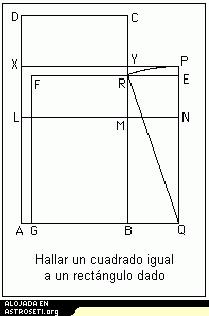
Considere el diagrama de la derecha: Dado el rectángulo ABCD, se marca L sobre AD de manera que AL = AB. Se completa entonces el cuadrado ABML. Bisecar ahora LD en X y se divide el rectángulo LMCD en dos rectángulos iguales mediante la línea XY. Mover ahora el rectángulo XYCD a la posición MBQN. Completar el cuadro AQPX. El cuadrado que acabamos de construir no es el que necesitamos y hace falta un poco más de trabajo para terminar. Rotar PQ sobre Q para que toque a BY en R. Luego QP = QR y vemos que es esta una ‘soga’ de construcción ideal. Dibuje ahora RE paralelo a YP y complete el cuadrado QEFG. Este es el cuadrado que buscamos y que es igual al rectángulo ABCD. El Sulbasutra de Baudhayana no ofrece ninguna demostración de este resultado (ni ningún otro de esa clase) pero podemos ver que es verdadero usando el teorema de Pitágoras.

EQ² = QR² + RE² = QP² + YP² = ABYX + BQNM = ABYX + XYCD = ABCD

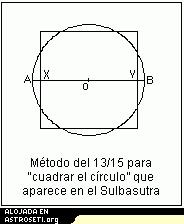
Todos los Sulbasutras contienen un método para la cuadratura del círculo. Es un método aproximado basado en la construcción de un cuadrado de lado ¹³/₁₅ veces el diámetro de un círculo dado, tal como se muestra en el diagrama de la izquierda. Esto se corresponde con tomar π = 4 × (¹³/₁₅)² = ⁶⁷⁶/₂₂₅ = 3.00444, que no es una aproximación muy buena. Desde luego no es tan buena como la que conocían mucho antes los babilónicos. Cabe destacar que en los Sulbasutras aparecen muchos valores diferentes de π, incluso varios diferentes en el mismo texto. Esto no es sorprendente pues siempre que se da una construcción aproximada se implica a algún valor de π. Los autores pensaban en términos de construcciones aproximadas y no de construcciones exactas, con un π para el que sólo tenían un valor aproximado. Por ejemplo, en el Sulbasutra de Baudhayana, igual que aparece el valor ⁶⁷⁶/₂₂₅ también lo hace ⁹⁰⁰/₂₈₉ y ¹¹⁵⁶/₃₆₁. En los diferentes Sulbasutras aparecen los valores 2.99, 3.00, 3.004, 3.029, 3.047, 3.088, 3.1141, 3.16049 y 3.2022 (ver [6]). En [3] el valor de π = ²⁵/₈ = 3.125 se encuentra en el Sulbasutra de Manava. En [9], además de examinar el problema de cuadrar el círculo tal como lo da Apastamba, el autor examina el problema de dividir un segmento en siete partes iguales, algo que pasa en el mismo Sulbasutra.

Considere el diagrama de la derecha. Los Sulbasutras también examinan el problema contrario de hallar un círculo de área igual a un cuadrado dado. Aparece la siguiente construcción. Dado el cuadrado ABCD, hallar el centro O. Rotar OD hasta la posición OE, donde E es el punto medio del lado DC del cuadrado. Sea Q el punto sobre PE tal que PQ es un tercio de PE. El círculo requerido tiene centro O y radio OQ. De nuevo es interesante calcular qué valor de π va implícito aquí para darse cuenta de lo exacta que es la construcción. Ahora bien, si el cuadrado tiene de lado 2a entonces el radio del círculo es r, donde

r = OE - EQ = √2a - ²/₃ (√2a - a) = a(^√2/₃ + ²/₃).

Entonces 4a² = πa² (^√2/₃ + ²/₃)² lo que da π = 36 / (√2 + 2)² = 3.088. Como vistazo final a las matemáticas de los Sulbasutras examinamos lo que podría ser lo más destacable. Tanto el Sulbasutra de Apastamba como el Katyayana dan la siguiente aproximación a √2:

Añade a la unidad de longitud su tercera parte y a esta tercera parte su propia cuarta parte menos la trigésimo cuarta parte de ese cuarto.

Ahora bien, esto da:

√2 = 1 + ¹/³ + ¹/_{(3 × 4)} - ¹/_{(3 × 4 × 34)} = ⁵⁷⁷/₄₀₈

que da, con nueve cifras decimales, 1.414215686. Comparado con el valor correcto de √2 = 1.414213562, se ve que el Sulbasutra de Apastamba tiene el resultado correcto hasta la quinta cifra decimal. Por supuesto que no se da ninguna indicación de como los autores de los Sulbasutras consiguen este resultado tan destacable. En 1932, Datta hizo una bonita sugerencia de cómo podría haberse alcanzado esta aproximación.

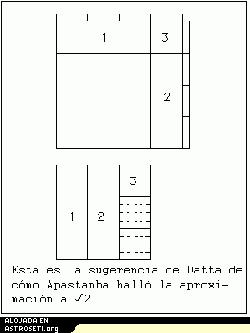En [1], Datta considera un diagrama como el de la derecha. La razón más probable para la construcción era crear un altar el doble de grande que otro ya construido. La sugerencia de Datta implica tomar dos cuadrados, trocear el segundo y montarlo alrededor del primero para obtener un cuadrado el doble de grande. Así tendríamos un lado de √2. El segundo cuadrado se corta en tres tiras iguales, colocando las tiras 1 y 2 alrededor del primer cuadrado como se indica en el diagrama. De la tercera tira sacamos un cuadrado cortando la parte superior y colocándolo en la posición 3. Tenemos ahora un nuevo cuadrado pero nos queda algo del segundo cuadrado que todavía tiene que montarse alrededor del primero. Se corta la parte restante (dos tercios de una tira) en 8 tiras iguales y las disponemos alrededor del cuadrado que estamos construyendo como se muestra en el diagrama. Ahora hemos usado todas las partes del segundo cuadrado pero la nueva figura que hemos construido no es un cuadrado completo ya que le falta una pequeña esquina cuadrada. Merece la pena destacar que el lado de este ‘cuadrado sin completar’ es

1 + ¹/₃ + ¹/_{(3 × 4)}

que, naturalmente, son los primeros términos de la aproximación. Ahora Datta argumenta en [1] que para mejorar este ‘cuadrado sin completar’ los autores de los Sulbasutras podrían haber calculado el ancho de la tira que se necesita cortar del lado izquierdo y del inferior para llenar la parte que falta. Esta tira tendría un área de (¹/₁₂)². Si x es el ancho que se corta, entonces:

2 × x × (1 + ¹/₃ + ¹/₁₂) = (¹/₁₂)²

esto nos da que x = ¹/_{(3 × 4 × 34)} que es aproximadamente 0.002450980392. Tenemos ahora un cuadrado cuyo lado tiene una longitud de:

1 + ¹/₃ + ¹/_{(3 × 4)} - ¹/_{(3 × 4 × 34)}

que es exactamente la aproximación dada por el Sulbasutra de Apastamba. Naturalmente hemos hecho una aproximación ya que las dos tiras de ancho x que hemos cortado se superponen en un cuadrado de lado x en la esquina inferior izquierda. Si tuviéramos esto en cuenta hubiéramos obtenido la ecuación:

2 × x × (1 + ¹/₃ + ¹/₁₂) - x² = (¹/₁₂)²

lo que nos lleva a un valor de x = ¹⁷/₁₂ - √2 que es aproximadamente igual a 0.002453105. Queda claro que no podemos tomar este camino ya que hemos llegado a un valor de x que implica a √2, ¡qué es precisamente la cifra a la que nos tratamos de aproximar! En [4] Gupta ofrece una forma más sencilla de obtener una aproximación de √2 que la dada por Datta en [1]. Emplea la interpolación lineal para obtener los dos primeros términos, corrige entonces estos dos términos para obtener el tercero para luego corregir esos tres términos y obtener así el cuarto. Aunque el método de Gupta es más sencillo (además de una interesante contribución) sin lugar a dudas hay algo atractivo en el argumento de Datta y algún tipo de sensación de que éste corresponde al espíritu de los Sulbasutras. Está claro que el método usado por estos matemáticos es muy importante para entender la profundidad de las matemáticas que se produjeron en la India a mediados del primer milenio antes de Cristo. Si seguimos la sugerencia de algunos historiadores de que los autores de los Sulbasutras simplemente copiaron una aproximación que ya conocían los babilónicos, podríamos llegar a la conclusión de que los matemáticos indios de este período estaban bastante menos avanzados de lo que se puede pensar si seguimos la sugerencia de Datta. Artículo de: J J O’Connor y E F Robertson MacTutor History of Mathematics Archive Bibliografía

1. B Datta, The science of the Sulba (Calcutta, 1932).
2. G G Joseph, The crest of the peacock (London, 1991).
3. R C Gupta, New Indian values of π from the Manava sulba sutra, Centaurus 31 (2) (1988), 114-125.
4. R C Gupta, Baudhayana’s value of √2, Math. Education 6 (1972), B77-B79.
5. S C Kak, Three old Indian values of π, Indian J. Hist. Sci. 32 (4) (1997), 307-314.
6. R P Kulkarni, The value of π known to Sulbasutrakaras, Indian J. Hist. Sci. 13 (1) (1978), 32-41.
7. G Kumari, Some significant results of algebra of pre-Aryabhata era, Math. Ed. (Siwan) 14 (1) (1980), B5-B13.
8. A Mukhopadhyay and M R Adhikari, The concept of cyclic quadrilaterals : its origin and development in India (from the age of Sulba Sutras to Bhaskara I, Indian J. Hist. Sci. 32 (1) (1997), 53-68.
9. A E Raik and V N Ilin, A reconstruction of the solution of certain problems from the Apastamba Sulbasutra of Apastamba (Russian), in A P Juskevic, S S Demidov, F A Medvedev and E I Slavutin, Studies in the history of mathematics 19 ‘Nauka’ (Moscow, 1974), 220-222; 302.

http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Indian_sulbasutras.html