Historia de la numeración en la India
Traductor : Javier de la GuardiaSupervisor : hypatia
Fecha publicación Astroseti :02-May-2007
Fecha articulo original :01-Nov-2000
Merece la pena comenzar este artículo con la misma cita de Laplace que usamos en el artículo en el que dimos una primera revisión de las matemáticas indias.
Laplace escribió:
El ingenioso método de expresar cada número posible utilizando un conjunto de diez símbolos (cada uno de ellos con un valor en su posición y un valor absoluto), surgió en la India. La idea parece hoy en día tan simple que su significado y profundidad no son apreciados en su justa medida. Su simplicidad subyace en el modo en el que facilitó el cálculo y colocó la aritmética en la primera posición entre las invenciones más útiles. La importancia del invento se aprecia con más facilidad cuando se considera que estaba mucho más allá que las ideas de dos de los mayores hombres de la antigüedad, Arquímedes y Apolonio.El propósito de este artículo es intentar la difícil tarea de describir el cómo los indios desarrollaron este sistema tan ingenioso. Examinaremos dos aspectos diferentes de los sistemas numerales indios. Comenzaremos estudiando la forma en la que los numerales 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 evolucionaron en lo que conocemos hoy. Por supuesto es importante apuntar que no existe una forma estándar de escribir estos numerales. Los diferentes tipos de letra instalados en este ordenador pueden crear diferentes aspectos de estos números, que aunque reconocibles, difieren los unos de los otros. Incluso son difíciles de reconocer en algunas versiones escritas a mano alzada.
El segundo aspecto que analizaremos de los numerales indios es el sistema de lugares y valores (posición-valor), que en los comentarios de Laplace con los que comenzábamos parece 'tan simple que su significado y profunda importancia no es apreciada en todo su valor'. Debemos apuntar el hecho, importante en ambos aspectos, que los sistemas numerales indios están basados casi en exclusiva en base 10, en oposición a los babilónicos que estaban en base 60.
Comenzando con los propios numerales, sabemos con certeza que los símbolos empleados hoy día son similares a los que se tenían en Europa en el siglo XV. Fue el avance de la imprenta lo que provocó la estandarización de esos símbolos. Sin embargo no debemos olvidar que muchos países utilizan hoy símbolos bastante diferentes del 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 y, al menos que se aprendan, esos símbolos resultan totalmente irreconocibles; como por ejemplo el alfabeto griego resulta ininteligible para alguien que no esté familiarizado con él.
Una de las fuentes de información más importantes que tenemos de los numerales indios procede de al-Biruni. Durante la década de 1020, al-Biruni visitó varias veces la India. Antes de ir allí ya sabía algo de la astronomía y las matemáticas indias gracias a las traducciones árabes de algunos textos sánscritos. Hizo un estudio detallado de la filosofía hindú y analizó varias ramas de las ciencias y las matemáticas indias. Al-Biruni escribió 27 trabajos sobre India y sobre diferentes áreas de su ciencia. En particular su recopilación sobre la astronomía india y sus matemáticas fue una valiosa contribución al estudio de la ciencia en India. Refiriéndose a los numerales indios en un famoso libro escrito alrededor de 1030, comenta:
Mientras que nosotros usamos letras para los cálculos de acuerdo con su valor numérico, los indios no las usan en absoluto para la aritmética. Y como las letras que usan para escribir son diferentes en diferentes regiones de su país, también lo son los números.Es razonable preguntarse dónde se originaron los diferentes símbolos para los números que vio al-Biruni. Los historiadores les siguen la pista hasta los numerales Brahmi que comenzaron a aparecer alrededor de la mitad del siglo III a. C. Estos numerales Brahmi no eran sólo símbolos para los números entre el 1 y el 9. La situación es mucho más complicada porque no eran un sistema de colocación según su valor (posición-valor) sino que eran símbolos usados para describir otros muchos números. Además no había símbolos especiales para el 2 y el 3 que se formaban a partir del símbolo 1.
Aquí están los Brahmi uno, dos, tres...
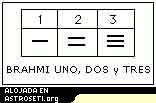
|
 Imagen original Imagen original |
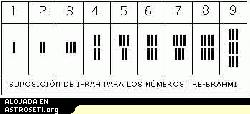
Había símbolos separados Brahmi para el 4, 5, 6, 7, 8, 9 y también había símbolos para 10, 100, 1000, ... al igual que para 20, 30, 40, ..., 90 y 200, 300, 400, ..., 900.
Los numerales Brahmi se han encontrado en cuevas y en monedas en regiones cercanas a Poona, Bombay y Uttar Pradesh. La datación de estos numerales nos indica que se emplearon bastante tiempo, hasta bien entrado el siglo IV. Por supuesto distintas inscripciones difieren en el estilo de los símbolos.
Aquí tenemos un estilo de los numerales Brahmi.

|
 Imagen original Imagen original |
Ahora debemos mirar delante y detrás en el tiempo en relación a la apariencia de los numerales Brahmi. Hacia delante llegamos a muchas formas diferentes de numerales pero entre ellas tenemos que escoger únicamente el camino que nos lleva a los símbolos que empleamos hoy en día. En primer lugar, sin embargo, debemos mirar a las diferentes teorías concernientes al origen de los numerales Brahmi.
No hay ningún problema en comprender los símbolos para 1, 2 y 3. Sin embargo los símbolos para 4, ..., 9 no parecen tener nada que ver con los números que representan. Ha habido innumerables teorías presentadas a lo largo de los años por los historiadores para explicar el origen de estos numerales. En [1] Ifrah lista un número de hipótesis que han sido presentadas.
- Los numerales Brahmi proceden de la cultura del valle del Indo de alrededor del año 2.000 a. de C.
- Los numerales Brahmi proceden de los numerales arameos.
- Los numerales Brahmi proceden del alfabeto Karoshthi.
- Los numerales Brahmi proceden del alfabeto Brahmi.
- Los numerales Brahmi proceden de un alfabeto numeral temprano posiblemente debido a Panini.
- Los numerales Brahmi proceden de Egipto.
I, II, III, X, IX, IIX, IIIX, XX.Ifrah examina todas y cada una de las seis hipótesis por turno y las rechaza, aunque hay que reconocer que en algunos casos se debe más bien a la falta de evidencias positivas que por falta de ellas.
Ifrah propone su propia teoría en [1]:
... los primeros nueve numerales Brahmi son los vestigios de una notación numérica indígena, en la que los nueve numerales estaban representados por su correspondiente número de líneas verticales... para hacer que los numerales pudieran escribirse de forma rápida estos grupos de líneas evolucionaron de forma similar a como lo hicieron los numerales del Egipto faraónico. Teniendo en cuenta el material en el que se escribía en la India (corteza de árbol u hojas de palmera) y las limitaciones de los instrumentos de escritura (cálamo o pinceles), la forma de los numerales se convirtió en algo muy complejo con numerosas uniones, hasta que perdieron cualquier parecido con los símbolos prototípicos.Una teoría muy bonita, que incluso podría ser cierta, pero que no cuenta con ninguna evidencia positiva en su favor. La idea es que evolucionaron de:

|
 Imagen original Imagen original |
Se podrían esperar evidencias de esta supuesta evolución si hallásemos otros numerales en algún lugar. Sin embargo parece que nunca encontraremos pruebas convincentes del origen de los numerales Brahmi.
Si examinamos la vía que nos lleva de los numerales Brahmi a nuestros símbolos presentes (e ignoramos los otros muchos sistemas que evolucionaron a partir de ellos), nuestro siguiente paso serían los símbolos Gupta. El período Gupta se llama así porque durante esos años la dinastía Gupta gobernaba en el estado de Magadha situado al noreste de la India. Fue entre los primeros años del siglo IV a. C. y los últimos del siglo VI a. C. Los numerales Gupta se desarrollaron a partir de los numerales Brahmi y se extendieron por grandes áreas del imperio Gupta según aumentaba el tamaño de su territorio.

|
 Imagen original Imagen original |
Los numerales Gupta se transformaron en los numerales Nagari, llamados también algunas veces numerales Devnagari. Estas formas evolucionadas de los numerales Gupta comenzaron a verse alrededor del siglo VII a. C. y continuaron hasta el siglo XI y más allá. Literalmente su nombre significa 'escritura de los dioses' y estaban considerados como los más bellos. Por ejemplo, al-Biruni escribe:
Lo que nosotros (los árabes) usamos como numerales es una selección de los mejores y más regulares números indios.
|
 Imagen original Imagen original |
Estos 'números más regulares' a los que se refiere al-Biruni son los numerales Nagari que habían sido transmitidos en aquella época al mundo árabe. La forma en la que los numerales indios se transmitieron entre los siglos VII al XVI se examina con detalle en [7]. En este documento, sin embargo, Gupta dice que los numerales indios habrían alcanzado el sur de Europa a finales del siglo V; pero su argumento se basa en la 'Geometría' de Boecio que ahora sabemos procede de la primera mitad del siglo XI. Parece muy poco probable que los numerales indios alcanzaran Europa tan temprano como sugiere Gupta.
Pasaremos ahora al segundo aspecto del sistema numeral indio que queremos examinar en este artículo, es decir: el hecho de que era un sistema de valor relativo a su posición en el que los numerales tenían diferentes valores dependiendo de su posición relativa con otros numerales. Aunque nuestro sistema de posición y valor es directo descendiente del indio, hay que destacar que los indios no fueron los primeros en desarrollar tal sistema. Los babilonios tenían un sistema de posición-valor tan temprano como en el siglo XIX a. C. pero este sistema estaba en base 60. Los indios fueron los primeros en desarrollar un sistema posicional en base 10 y considerando lo que hicieron los babilonios, éste surgió de forma muy tardía.
El documento indio más antiguo que contiene un número escrito en el sistema de posición-valor que usamos hoy en día es un documento legal fechado en 346 en el calendario Chhedi que se puede traducir como el 594 AD. Es un documento de alquiler de Dadda III de Sankheda en la región Bharukachcha. El único problema con este hallazgo es que algunos historiadores dicen que la fecha fue falsificada y añadida posteriormente. Aunque no era inusual que tales documentos fueran modificados en fecha posterior para que la propiedad a la que hacían referencia pudiera ser reclamada por alguien que no era el auténtico propietario, no parece razonable que tuviera que ser falsificada en este caso. Por otra parte, a pesar de las dudas, podemos estar razonablemente seguros que este documento proporciona evidencia de que un sistema de posición-valor se utilizaba en la India a finales del siglo VI.
Se han encontrado muchos otros contratos de alquiler ya datados y que usan el sistema posición-valor bien para indicar la fecha u otros valores dentro del texto. Estos incluyen:
- Un contrato de alquiler de Dhiniki fechado en 794 en el calendario Vikrama, o en nuestro calendario en el 737.
- Una inscripción de Devendravarman fechada en 675 del calendario Shaka, o en nuestro calendario en el 753.
- Un contrato del alquiler de Danidurga fechado en 675 en el calendario Shaka, o en nuestro calendario en el 737.
- Un contrato de alquiler de Shankaragana fechado en el 715 del calendario Shaka, o en nuestro calendario en el 793.
- Un contrato de alquiler de Nagbhata fechado en el 872 del calendario Vikrama, o en nuestro calendario en el 815.
- Una inscripción de Bauka fechada en el 894 del calendario Vikrama, o en 837 en nuestro calendario.
La primera inscripción fechada y no discutida está en Gwalior en 933 del calendario Vikrama, nuestro año 876. Hay más detalles sobre esta inscripción en el artículo sobre la historia del cero.
Hay evidencia indirecta que los indios desarrollaron un sistema posicional de números tan pronto como en el siglo I. La evidencia se encuentra en inscripciones que, aunque no en la India, se han encontrado en países que asimilaron la cultura india. Otra fuente es el manuscrito Bakhsali que contiene números escritos en notación posición-valor. El problema radica en la fecha de datación del manuscrito, un tópico que examinamos en detalle en nuestro artículo sobre el mismo.
Nos queda, por supuesto, la pregunta de por qué los indios desarrollaron tan ingenioso sistema mientras que los antiguos griegos, por ejemplo, no lo hicieron. Se ha intentado explicar mediante varias teorías. Algunos historiadores creen que el sistema de posición-valor en base 60 babilonio se transmitió a los indios a través de los griegos. Comentamos en el artículo sobre la historia del cero cómo los astrónomos griegos que usaban el sistema en base 60 de los babilonios utilizaban un símbolo parecido a nuestro cero. La teoría plantea que estas ideas fueron transmitidas a los indios quienes entonces las combinaron con su propio sistema numeral en base 10 que había existido en la India durante largo tiempo.
Una segunda hipótesis es que la idea de posición-valor en los sistemas numerales indios procede de los chinos. En particular, los chinos tenían varas numéricas con valor pseudo-posicional que, según algunos, se convirtieron en la base del sistema posicional indio. Esta visión es defendida por ejemplo por Lay Yong Lam; véase [8]. Lam argumenta que el sistema chino ya contenía lo que el llama los:
...tres elementos esenciales de nuestro sistema de notación numérico: (i) nueve signos y el concepto del cero (ii) un sistema de posición-valor (iii) y una base decimal.Una tercera hipótesis es avanzada por Joseph en [2]. Su idea es que la posición-valor en los sistemas numerales indios es algo que fue desarrollado exclusivamente por los propios indios. Tiene una interesante teoría sobre el por qué los indios llegaron a ese desarrollo. La razón, según Joseph, se debe a la fascinación india por los números grandes. Freudenthal es otro historiador de las matemáticas que apoya la teoría de que la idea es enteramente india.
Para ver claramente esta temprana fascinación india por los números grandes podemos echar un vistazo al 'Lalitavistara', un relato de la vida de Gautama Buddha. Es difícil datar este trabajo porque estuvo en continuo desarrollo durante un largo período de tiempo, pero es razonable suponer que fue escrito alrededor de los siglos I y II. En el 'Lalitavistara', Gautama,
cuando es joven es examinado en matemáticas. Se le pide que nombre todos los rangos numéricos más allá de un koti que es 107 . Él lista todas las potencias de 10 hasta 1053 . Tomando esto como un primer nivel sigue a continuación a un segundo nivel y alcanza eventualmente 10421 . El examinador de Gautama dice:
Tú, y no yo, eres el maestro de las matemáticas.Son historias como esta las que convencen a Joseph que la fascinación de los indios por los números grandes es lo que les condujo a inventar un sistema en el que tales números se pudieran expresar fácilmente, es decir una notación basada en el valor asociado a la posición. escribe en [2]:
El uso temprano de tales números grandes condujo eventualmente a la adopción de series de nombres de números para las sucesivas potencias de diez. La importancia de estos nombres de números no puede minimizarse. El sistema numeral con palabras fue reemplazado más tarde por una notación alfabética, el lógico avance de proceder con múltiplos de diez [...] el sistema decimal de posición-valor, se adoptó para poder ser asociado con el valor de los lugares de los números cuando estaban ordenados de izquierda a derecha o viceversa. Y esto fue precisamente lo que sucedió en la India.Sin embargo, la misma historia en el 'Lalitavistara' convence a Kaplan (ver [3]) de que las ideas de los números para los indios proceden de los griegos, ya que para él la historia es una versión india del 'Contador de arena' de Arquímedes. Todo lo que sabemos es que el sistema de posición-valor de los indios, aunque original, fue transmitido a los árabes y más tarde a Europa para tener, en palabras de Laplace, 'gran importancia' en el desarrollo de las matemáticas.
Artículo de: J J O'Connor y E F Robertson
MacTutor History of Mathematics Archive
Bibliografía
- G Ifrah, A universal history of number : From prehistory to the invention of the computer (London, 1998).
- G G Joseph, The crest of the peacock (London, 1991).
- R Kaplan, The nothing that is : a natural history of zero (London, 1999).
- L C Karpinski, The history of arithmetic (New York, 1965).
- K W Menninger, Number words and number symbols : A cultural history of numbers (Boston, 1969).
- D E Smith and L C Karpinski, The Hindu-Arabic numerals (Boston, 1911).
- R C Gupta, Spread and triumph of Indian numerals, Indian J. Hist. Sci. 18 (1) (1983), 23-38.
- L Y Lam, Linkages : exploring the similarities between the Chinese rod numeral system and our numeral system, Arch. Hist. Exact Sci. 37 (4) (1987), 365-392.
- J S Pettersson, Indus numerals on metal tools, Indian J. Hist. Sci. 34 (2) (1999), 89-108.
- R K Sarma, A note on the use of words for numbers in ancient Indian mathematics, Math. Education 7 (1973), A44-A45.
- K Vogel, Uses of letters and Indian numerals in Byzantium (Greek), Neusis No. 5 (1996), 75-81; 170.
AstroPortal 3.0 Desarrollado por 4lgx
visitas únicas desde 13/07/2007
Ver nuestras estadísticas