Uno de los primeros artículos incluidos en la sección ‘Tópicos de historia’ de nuestro archivo web fue sobre la historia de π. Es un artículo muy popular y ha provocado que muchos lectores nos pidieran un artículo similar sobre el número e. Hay un gran contraste entre los desarrollos históricos de estos dos números y de alguna manera escribir la historia de e es una tarea mucho más complicada que escribir la de π. El número e es, comparado con π, un arribo reciente en la escena matemática. El número e llega por primera vez a las matemáticas de forma muy discreta. Sucedió en 1618 cuando, en un apéndice al trabajo de Napier sobre logaritmos, apareció una tabla dando el logaritmo natural de varios números. Sin embargo, no se reconoció que estos fueran logaritmos en base e, ya que la base sobre la que se calculan los logaritmos no surgió en la manera en la que se pensaba en los logaritmos en aquel entonces. Aunque hoy consideramos a los logaritmos como los exponentes a los que se debe elevar una base para obtener el número deseado, esta es una forma moderna de pensar.
Regresaremos después a este punto. Dicha tabla en el apéndice, aunque no tiene el nombre del autor, es casi seguro que fue escrita por Oughtred. Unos años después, en 1624, e estuvo a punto de volver a la literatura matemática pero no lo logró. En ese año, Briggs dio una aproximación numérica al logaritmo base diez de e sin mencionar a e específicamente en su trabajo. La siguiente posible aparición de e es de nuevo dudosa. En 1647, Saint-Vincent calculó el área bajo una hipérbola rectangular. Si reconoció o no la conexión con los logaritmos es debatible y, aún si lo hubiera hecho, no había realmente razón para que se encontrara explícitamente con el número e. Sin lugar a dudas, hacia 1661 Huygens comprendió la relación entre la hipérbola rectangular y el logaritmo. Examinó explícitamente la relación entre el área bajo la hipérbola rectangular yx = 1 y el logaritmo. Por supuesto, el número e es tal que el área bajo la hipérbola rectangular entre 1 y e es igual a 1. Ésta es la propiedad que hace que e sea la base de los logaritmos naturales pero los matemáticos de la época no lo entendían, aunque se estaban acercando lentamente a ello. Huygens hizo otro avance en 1661. Definió una curva a la que llamó ‘logarítmica’ pero no en los términos en los que nosotros nos referimos a una curva exponencial, con la forma y = kax . Nuevamente, a partir de esto sale el logaritmo base 10 de e, que Huygens calculó a 17 decimales. Sin embargo, en su trabajo aparece como el cálculo de una constante y no es reconocida como el logaritmo de un número (cerca otra vez pero e sigue sin ser reconocido). Hay trabajos posteriores sobre los logaritmos en los que todavía no aparece el número e como tal pero que contribuyen al desarrollo de los logaritmos. En 1668, Nicolás Mercator publicó Logarithmotechnia que contiene la expansión en serie de log (1+ x ). En este trabajo, Mercator usa el término ‘logaritmo natural’ por primera vez para los logaritmos en base e. El número e otra vez no aparece explícitamente y continúa escondido en las cercanías. Talvez de manera sorprendente, ya que los trabajos sobre los logaritmos habían estado tan cerca de reconocer al número e, la primera vez en que e es ‘descubierto’ no tiene que ver con la noción de logaritmo sino más bien en un estudio del interés compuesto.
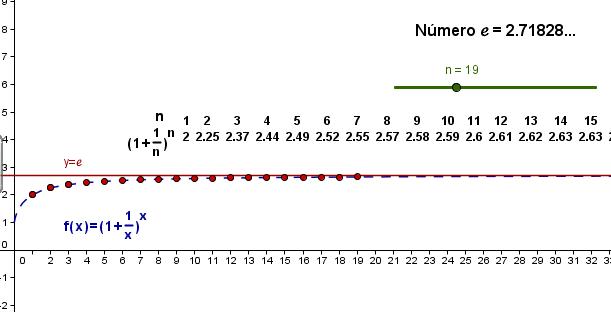
En 1683, Jacobo Bernoulli examinó el problema del interés compuesto y, durante su análisis del interés compuesto continuamente, trató de encontrar el límite de (1 + 1/n)n cuando n tiende a infinito. Usó el teorema del binomio para demostrar que el límite tenía que estar entre 2 y 3, por lo que podríamos considerar que esta es la primera aproximación que se encontró para e. También, si aceptamos ésta como una definición de e, sería la primera vez en que un número fue definido mediante un proceso de límite. De hecho, Bernoulli no reconoció en ningún momento la conexión entre su trabajo y aquellos sobre los logaritmos. Mencionamos arriba que, al inicio de su desarrollo, no se pensaba que los logaritmos tuvieran relación alguna con los exponentes. Claro que de la ecuación x = at, deducimos que t = log x donde log es el logaritmo en base a pero esto es una forma de pensar muy posterior. Aquí realmente estamos pensando en log como una función mientras que los primeros trabajos sobre logaritmos lo consideraban meramente como un número que ayudaba en los cálculos. Es posible que el primero en comprender la manera en que la función log es la inversa de la función exponencial haya sido Jacobo Bernoulli. Por otro lado, la primera persona que hizo la conexión entre logaritmos y exponentes puede haber sido James Gregory. En 1684, sin duda reconoció esta conexión pero podría no haber sido el primero. Hasta donde sabemos, la primera vez que el número e aparece explícitamente es en 1690.
En ese año, Leibniz le escribió una carta a Huygens en la que usa la notación b para lo que nosotros hoy llamamos e. Por fin el número e tenía nombre (aunque no sea el actual) y era reconocido. El lector puede preguntarse, no sin cierta razón, por qué no empezamos este artículo sobre la historia de e en el punto en el que hace su primera aparición. La razón es que, aunque los trabajos descritos antes nunca consiguieron exactamente identificar a e, una vez que se le identificó, entonces se dieron cuenta poco a poco de que los trabajos anteriores son importantes. En retrospectiva, los desarrollos iniciales del logaritmo forman parte de la comprensión del número e. Más arriba se mencionaron los problemas que surgen del hecho de que no se pensara en log como una función. Es necesario mencionar que Johann Bernoulli comenzó el estudio del cálculo de la función exponencial en 1697 cuando publicó Principia calculi exponentialium seu percurrentium. Este trabajo incluye el cálculo de varias series exponenciales y muchos resultados se obtienen mediante integración término a término. Es tanta la notación matemática actual que le debemos a Euler que no sorprende descubrir que la notación e para este número se la debemos a él. La afirmación que se ha hecho algunas veces de que Euler usó la letra e porque era la primera letra de su nombre es ridícula.
Es probable que e ni siquiera venga de ‘exponencial’ sino que sea simplemente la vocal que sigue de la a, la cual Euler ya estaba usando en su trabajo. Sea cual fuera la razón, la notación e aparece por primera vez en una carta que le escribió Euler a Goldbach en 1731. Euler hizo varios descubrimientos respecto a e en los años siguientes pero no fue sino hasta 1748 con la publicación de Introductio in Analysin infinitorum cuando Euler dio un tratamiento completo a las ideas alrededor de e. Demostró que e = 1 + 1/1! + 1/2! + 1/3! +… y que e es el límite de (1 + 1/n)n cuando n tiende a infinito. Euler dio una aproximación de e con 18 decimales, e = 2.718281828459045235 sin decir de dónde salió. Es probable que haya calculado el valor él mismo, pero de ser así no hay indicios de cómo lo hizo. De hecho, tomando unos 20 términos de 1 + 1/1! + 1/2! + 1/3! +… se obtiene la aproximación dada por Euler. Entre otros resultados interesantes, en este trabajo está la relación entre las funciones seno y coseno y la función exponencial compleja, lo cual Euler dedujo usando la fórmula de De Moivre. Es interesante que Euler también haya dado el desarrollo de e en fracciones continuas y que haya notado un patrón en la expresión. Específicamente dio #1# y #2# Euler no dio una prueba de que los patrones que encontró continuaran (lo cual sí sucede) pero sabía que si diera esta prueba sería equivalente a probar que e es irracional. Ya que, si la fracción continua para (e -1)/2 siguiera el patrón mostrado por los primeros términos, 6,10, 14,18, 22, 26,… (sumando cuatro cada vez), entonces nunca terminaría; por ello (e -1)/2 (así como e) no puede ser racional. Esto sin duda podría considerarse como el primer intento de probar que e no es racional. Aquella pasión que llevó a tantos a calcular π con más y más decimales nunca se dio para el caso de e. Sin embargo, sí hubo quienes calcularon su expansión decimal y el primero en dar e con un gran número de dígitos fue Shanks en 1854. Vale la pena hacer notar que Shanks fue aún más entusiasta calculando la expansión decimal de p. Glaisher mostró que las primeras 137 posiciones de los cálculos de Shanks estaban correctas pero encontró un error que, después de ser corregido por Shanks, dio e con 205 decimales. De hecho, se necesitan unos 120 términos de 1 + 1/1! + 1/2! + 1/3! +… para obtener 200 decimales de e. En 1864, Benjamín Peirce se tomó una foto parado delante de un pizarrón en el que había escrito la fórmula i - i = √(eπ).
En sus clases, decía a sus estudiantes Señores, no tenemos la menor idea de lo que significa esta ecuación pero podemos estar seguros de que su significado es algo muy importante. Casi todo el mundo acepta que Euler fue el primero en probar que e es irracional. Y sin duda fue Hermite quien probó en 1873 que e no es un número algebraico. Si ee es algebraico es todavía una pregunta abierta, aunque claro que lo único que falta es una prueba - ¡ningún matemático consideraría seriamente que ee es algebraico! Hasta donde sabemos, lo más cerca que los matemáticos han llegado a probarlo es un resultado reciente que dice que al menos uno de estos dos números es trascendente: ee y e elevado a la potencia e2. Más cálculos de la expansión decimal siguieron. En 1884 Boorman calculó e con 346 decimales y encontró que su cálculo coincidía con el del Shanks hasta la posición 187 pero después variaban. En 1887, Adams calculó el logaritmo base 10 de e con 272 decimales. Quien quiera ver a e con 10 000 decimales - mire aquí. Referencias
- E Maor, e : the story of a number Princeton, 1994.
- J L Coolidge, The number e, Amer. Math. Monthly 57, 1950, 591-602.
Autores: J J O’Connor y E F Robertson
http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/e.html