Astroseti.org

En esta segunda entrega profundizaremos en el argumento de Einstein y posteriores reacciones a lo largo de los años a este artículo.

1.3 La versión de Einstein del argumento

Einstein se puso casi inmediatamente a proporcionar una versión más clara y centrada del argumento. Comenzó este proceso solo unas pocas semanas más tarde de que el EPR fuese publicado, en la carta a Schrödinger del 19 de Junio, y continuó en un artículo publicado el año siguiente (Einstein 1936). Volvió sobre estas ideas algunos años más tarde en otras publicaciones. Aunque sus distintas exposiciones difieren unas de otras todas ellas emplean sistemas compuestos como forma de implementar medidas a distancia no perturbativas. Ninguno de los informes propios de Einstein contienen el Criterio de Realidad ni el torturado argumento EPR sobre cuándo los valores de una cantidad pueden ser considerados como “elementos de realidad”. El Criterio y estos “elementos” simplemente desaparecen. Tampoco Einstein se preocupó de cálculos, como los de Podolsky, sobre la forma explícita de la función de onda completa para el sistema compuesto. Además, el mismo 19 de Junio de 1935, logró aclarar que no estaba especialmente interesado en la cuestión de los valores simultáneos para cantidades incompatibles como posición y momento. La preocupación que expresó a Schrödinger se debía a la cuestión de completitud, dada por los recursos de la Teoría Cuántica, al describir la situación sobre una variable individual (tal vez posición, tal vez momento). Con respecto al tratamiento de un par incompatible le dice a Schrödinger "ist mir wurst" — literalmente, eso para mí es salchichón; es decir, le traía sin cuidado. (Fine 1996, p. 38). En sus siguientes escritos sobre EPR, Einstein investigó una incompatibilidad entre afirmar localidad y separabilidad, por una parte, y completitud en la descripción de sistemas individuales a través de funciones de estados, por otra. Su argumento es que podemos tener como mucho una de ellas, pero no ambas. Frecuentemente se refiere a este dilema como “paradoja”".

En la carta a Schrödinger del 19 de Junio, Einstein esboza un simple argumento para el dilema, aproximadamente como sigue. Considera una interacción entre los sistemas Albert y Niels que conservan sus posiciones relativas. (No tenemos que preocuparnos por el momento, o cualquier otra cantidad). Considera la función de ondas desarrollada para el sistema total (Albert+Niels). Ahora asume un principio de localidad-separabilidad (Einstein llama a esto Trennungsprinzip — principio de separación): Si una propiedad física se mantiene en el sistema de Niels no depende de qué medidas (si hay alguna) se han hecho localmente en el sistema de Albert. Si medimos la posición del sistema de Albert, la conservación de la posición relativa implica que podemos deducir inmediatamente la posición de Niels; es decir, podemos deducir que el sistema de Niels tiene una posición determinada. Por localidad-separabilidad se deduce que el sistema de Niels debe ya tener una posición determinada justo antes de que Albert comience dicha medida. En ese momento, sin embargo, el sistema de Niels no tiene una función de estado independiente. Solo hay una función de estado para el sistema combinado y la función de estado total no predice con certeza la posición en la que encontraríamos el sistema de Niels (es decir, no es un producto uno de cuyos factores es un eigenestado para la posición del sistema de Niels). Así pues la descripción del sistema de Niels proporcionada por la función de estado cuántico no es completa. Una descripción completa diría (definitivamente sí) si una propiedad física fuese cierta para el sistema de Niels. (Nótese que este argumento no depende de la reducción de la función de estado total para el sistema combinado). En esta formulación del argumento están claros los conflictos de localidad-separabilidad con el enlace eigenvalor-eigenestado, que sostiene que una cantidad de un sistema tiene un eigenvalor si y solo si el estado del sistema es un eigenestado de dicha cantidad con tan eigenvalor. La parte “solo si” del enlace necesitaría ser de orden más débil para interpretar las funciones de estado cuántico como descripciones completas.

Aunque este simple argumento concentra lo que vio Einstein como esencial, quitando la mayoría de detalles técnicos y distracciones, tenía otro argumento ligeramente más complejo al que también dedicó mucho esfuerzo. (Está en realidad enterrado en el artículo EPR, p. 779.) El segundo argumento se centra claramente en la interpretación de las funciones de estado cuántico y no en algún tema sobre valores simultáneos (reales o no) para cantidades incompatibles. Dice algo como esto.

Supón, como en el EPR, que las interacciones entre los dos sistemas conservan la posición relativa y un momento total cero y que los sistemas están muy separados. Como antes, podemos medir la posición o el momento del sistema de Albert y, en cualquier caso, podemos inferir la posición o momento para el sistema de Niels. Esto se deduce de la reducción del la función de estado total que, dependiendo de si medimos la posición o el momento en el sistema de Albert, el sistema de Niels dejará (respectivamente) un eigenestado de posición o un eigemestado de momento. Supón también que se mantiene la separabilidad para Niels; esto es, que el sistema de Niels tiene algún estado físico real de acontecimientos. Si además se mantiene la localidad, entonces la medida del sistema de Albert no perturba la “realidad” asumida para el sistema de Niels. Sin embargo, dicha realidad parece ser representada por funciones de estado bastante distintas, dependiendo de qué medidas se escogen tomar en el sistema de Albert. Si comprendemos una “descripción completa” para descartar esta y pueden describirse otros estados físicos con funciones de estado con distintas implicaciones físicas, entonces podemos concluir que la descripción de la Mecánica Cuántica es incompleta. Aquí de nuevo nos enfrentamos con un dilema entre separabilidad-localidad y completitud. Muchos años más tarde Einstein lo puso de esta forma (Schilpp 1949, p. 682):

La paradoja nos fuerza a renunciar a una de las dos afirmaciones siguientes:

• La descripción a través de la función-psi es incompleta


• El estado real de objetos espacialmente separados es independiente de cada uno de los otros

Parece que el punto central del EPR era argumentar que al interpretar la función de estado cuántico nos encontramos con estas alternativas.

Como hemos visto, al enmarcar sus propios argumentos EPR para la incompletitud de la Teoría Cuántica, Einstein hizo uso de la separabilidad y localidad que están tácitamente supuestas en el artículo EPR. Proporciona una afirmación clara de sus ideas aquí, en una carta a Max Born:

Esto es … una característica de … los objetos físicos que se piensa que están ordenados en un continuo espacio-tiempo. Un aspecto esencial de esta ordenación … es que hicieron la afirmación, en cierto momento, de la existencia independiente de uno y otro, proporcionando a estos objetos que "estén situados en distintas partes del espacio". … La siguiente idea caracteriza la independencia relativa de los objetos (A y B) distantes en el espacio: la influencia externa de A no tiene influencia directa sobre B”. (Born, 1971, pp. 170-71)

En el curso de su correspondencia con Schrödinger, sin embargo, Einstein se dio cuenta de que sus suposiciones sobre separabilidad y localidad no eran necesarias para llegar a la conclusión de incompletitud a la que llegó más tarde; es decir, para demostrar que la función de estado de un sistema no era una descripción completa del estado real del acontecimiento respecto al sistema. La separabilidad supone que hay un estado real de los acontecimientos (tras la separación de sistemas) y la localidad supone que no se puede influenciar directamente actuando a distancia. De lo que Einstein se dio cuenta fue que estas dos suposiciones eran ya parte de una concepción corriente de un objeto macroscópico. Así pues si se observa la interacción de un macrosistema con un microsistema no necesitaría enmarcar suposiciones adicionales para concluir que la descripción cuántica del total era incompleta con respecto a su parte microscópica. Escribiendo a Schrödinger el 8 de Agosto de 1935 Einstein dice que demostrará esto a través de “ejemplos macroscópicos ordinarios”.

El sistema es una sustancia en un equilibrio químicamente inestable, tal vez una carga de pólvora que, a través de fuerzas intrínsecas, puede estallar espontáneamente, y donde la vida media que abarca toda la configuración es de un año. En principio esta puede representarse fácilmente de forma mecánico-cuántica. Al principio la función-psi caracteriza un estado microscópico razonablemente bien definido, pero de acuerdo a tu ecuación [es decir, la ecuación de Schrödinger], pasado el transcurso de un año este no sigue siendo el caso. En lugar de eso, la función-psi describe un tipo de mezcla entre sistemas, uno que ya ha explotado y otro que aún no lo ha hecho. A través de ningún tipo de interpretación se puede convertir esta función-psi en una descripción adecuada de un estado real de los acontecimientos; en realidad simplemente no hay intermediario entre explotado y no explotado. (Fine 1996, p. 78)

La cuestión es que tras un año la pólvora explotará, o no. (Este es el “estado real de la situación” que en la situación EPR se requiere para asumir separabilidad). La función de estado, sin embargo, habrá evolucionado a una superposición más compleja sobre estas dos alternativas. Siempre que mantengamos la unión eigenestado-eigenvalor, la descripción cuántica a través de la función de estado no producirá ninguna conclusión, y por tanto la descripción cuántica es incompleta.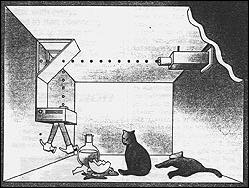

El lector puede reconocer la similitud entre este ejemplo de la pólvora explosiva y el gato de Schrödinger (Schrödinger 1935a, p. 812). En el caso del gato un átomo inestable está conectado a un dispositivo letal que, tras una hora, actuará envenenando (y matará) al gato o no, dependiendo de si el átomo decae. Tras una hora el gato está vivo o muerto, pero el estado cuántico del sistema completo átomo-veneno-gato en este momento es una superposición que involucra las dos posibilidades y, como en el caso de la pólvora, no hay una descripción completa de la situación (vida o muerte) del gato. La similitud entre la pólvora y el gato es difícilmente accidental dado que la primera aparición del ejemplo del gato de Schrödinger aparece en su respuesta del 19 de Septiembre de 1935 a la carta de la pólvora de Einstein del 8 de Agosto. Allí Schrödinger dice que él mismo ha construido “un ejemplo muy similar a su barril explosivo", y procede a esbozar el gato (Fine 1996, pp. 82-83). Aunque la “paradoja del gato” es habitualmente citada en conexión con los problemas de medida cuántica y tratado como una paradoja aparte de la EPR, su origen está aquí, como una versión compacta del argumento de incompletitud del EPR. El desarrollo de Schrödinger del “entrelazamiento”, el término que introdujo como descripción general para las correlaciones resultantes cuando interactúan sistemas cuánticos, también comienza en esta correspondencia sobre la EPR (Schrödinger 1935a, 1935b; ver Entrelazamiento cuántico e información).

2. Una forma popular del argumento: La respuesta de Bohr

La literatura que rodea a la EPR contiene aún otra versión del argumento, una versión popular que – al contrario que cualquiera de las de Einstein – caracteriza el Criterio de Realidad. Supón de nuevo una interacción entre nuestros dos sistemas que mantiene ambas posiciones relativas y un momento total de cero y supón que los sistemas se encuentran alejados. Si medimos la posición del sistema de Albert, podemos inferir que el sistema de Niels tiene una posición correspondiente. También podemos predecirlo con certeza, dado el resultado de la medida de la posición en el sistema de Albert. Así pues, de acuerdo con el Criterio de Realidad, la posición del sistema de Niels constituye un elemento de realidad. De forma similar, si medimos el momento en el sistema de Albert, podemos concluir que el momento en el sistema de Niels es un elemento de realidad. El argumento ahora concluye que dado que podemos elegir con libertad medir posición o momento, se “sigue” que ambos deben ser elementos de realidad simultáneamente.

Por supuesto tal conclusión no se desprende de nuestra libertad para elegir. No es suficiente ser capaces de elegir a nuestro antojo qué cantidad medir; para llegar a la conclusión siguiendo solo el Criterio sería necesario ser capaces de medir ambas cantidades a la vez. Este es precisamente el punto del que Einstein se percató en su carta a Ehrenfest en 1932 y que dirige al EPR suponiendo localidad y separabilidad. Lo que choca en esta versión es que estos principios, centrales para el argumento original del EPR y para el dilema del corazón de las versiones de Einstein, desaparece aquí. En lugar de esto, lo que tenemos es casi una caricatura del artículo EPR más que una seria reconstrucción. Desafortunadamente, quizá debido en parte a las dificultades presentadas por el texto de Podolsky, este es el argumento más comúnmente citado en la literatura física y atribuido a la misma EPR. Podolsky, sin embargo, no debería llevarse toda la culpa. Para esta versión del texto de Podolsky hay una fuente prominente, en términos que uno puede entender más fácilmente su popularidad entre los físicos. La fuente es el mismo Niels Bohr.

En la época del artículo de EPR se habían librado muchas otras batallas acerca de las primeras interpretaciones de la Teoría Cuántica, al menos para satisfacción de los físicos que trabajaban en ello. Bohr había emergido como el “filósofo” de la nueva teoría y la comunidad de teóricos cuánticos, ocupada con el desarrollo y extensión de la teoría, se mostraron felices de seguir el liderazgo de Bohr cuando vino a explicar y defender su base conceptual (Beller 1999, Capítulo 13). De esta forma en 1935 la carga estaba sobre Bohr en intentar explicar qué estaba mal en la “paradoja” EPR. El artículo principal que escribió para descargarse de este peso (Bohr 1935a) se convirtió en el canon de cómo responder al EPR. Desgraciadamente, el resumen de Bohr del EPR en este artículo, la cual es la versión justo de arriba, también se convirtió en el canon de lo que contenía el EPR en su forma argumental.

La respuesta de Bohr al EPR comienza, como hacen muchos de los tratados de temas conceptuales que aparecen con la Teoría Cuántica, con una discusión sobre las limitaciones de las determinaciones simultáneas de posición y momento. Como es habitual, son descritas desde un análisis de las posibilidades de medida si se usa un aparato que consta de un diafragma conectado a un marco rígido. Bohr enfatiza que la cuestión es hasta qué punto podemos rastrear la interacción entre las partículas medidas y el instrumento de medida. (Ver Beller 1999, Capítulo 7 para un análisis detallado y discusión de las “dos voces” contenidas en el texto de Bohr.) Siguiendo con el resumen del EPR, Bohr (1935a, p. 700) se centra en el Criterio de Realidad el cual, dice Bohr, “contiene una ambigüedad respecto al significado de la expresión ‘sin perturbación de ningún tipo en el sistema’". Bohr concede que la medida indirecta del sistema de Niels lograda cuando se hace una medida en el sistema de Albert no involucra ninguna “perturbación mecánica” del sistema de Niels. Aún así, afirma que una medida en el sistema de Albert involucra “una influencia en las condiciones que definen los posibles tipos de predicciones considerando el comportamiento futuro del sistema [de Niels]". Lo que Bohr puede haber tenido en mente es que cuando, por ejemplo, medimos la posición en el sistema de Albert y obtenemos un resultado podemos predecir la posición del sistema de Niels con certeza. Sin embargo, medir la posición del sistema de Albert no nos permite una certeza similar en la predicción del momento del sistema de Niels. Lo contrario podría ser cierto habiendo medido el momento en el sistema de Albert. De esta forma, dependiendo de qué variable midamos en el sistema de Albert, seremos capaces de hacer distintas predicciones sobre los resultados de posteriores medidas en el sistema de Niels.

Hay dos cosas importantes que se deben hacer notar sobre esta respuesta. La primera es ésta. Concediendo que el método indirecto de Einstein para determinar, digamos, la posición del sistema de Niels, no perturba dinámicamente el sistema, Bohr aquí se desvía de su programa original de complementaridad, que estaba basada en las relaciones de incertidumbre y el carácter estadístico de la Teoría Cuántica en sistemas con perturbaciones físicas incontrolables, perturbaciones que se supone que aparecen inevitablemente en la medida de algunas variables del sistema. En lugar de esto Bohr distingue ahora entre una perturbación física (o "mecánica") y lo que se podría llamar una “perturbación informativa”; es decir, una perturbación en la información disponible para predecir el comportamiento futuro de un sistema. Enfatiza que solo la última es la que aparece en la situación del EPR.

El segundo dato importante a remarcar es cómo la respuesta de Bohr necesita ser implementada para bloquear el tipo de argumentos que favorecen a Einstein, la cual presenta un dilema entre los principios de localidad y completitud. En el argumento de Einstein el principio de localidad hace referencia explícita a la realidad del sistema no medido (sin influencia directa en la realidad de allí debido a las medidas hechas aquí). De ahí que el apunte de Bohr hacia una perturbación informativa no afectaría al argumento en absoluto a menos que se incluya la información disponible para predecir el comportamiento futuro de los sistemas no medidos como parte de la realidad del sistema. Esto sería poco plausible por dos razones. Primero, porque la información sobre el sistema no medido de Niels está disponible a aquello cercano al sistema de Albert, que está en algún lugar, y para sus contactos, dondequiera que estén. En segundo lugar, debido a que la idea de “información sobre el sistema de Niels” tendría menos sentido si lo que designamos como “sistema de Niels” incluye esta información. No obstante, este es el movimiento que parece hacer Bohr, manteniendo que las “condiciones” (que definen los posibles tipos de predicciones respecto al comportamiento futuro del sistema de Niels) “constituyen un elemento inherente en la descripción de cualquier fenómeno al cual el término “realidad física” pueda ser asociado de forma adecuada" (Bohr 1935a, p. 700). Para estar seguros, si incluimos información predictiva en la “realidad” del sistema no medido, entonces falla el principio de localidad (aunque podría mantenerse la separabilidad) y por tanto la inferencia de la EPR en la incompletitud de la Teoría Cuántica estaría bloqueada. Así pues, esta salida concede validad al argumento de la EPR y bloquea su impacto en el tema de la completitud extendiendo el concepto de realidad física de tal forma que hace a la Teoría Cuántica altamente no local.

A pesar del aparente apoyo de Bohr a las interacciones no-locales en su respuesta al EPR, en otros lugares Bohr rechaza la no-localidad en los términos más enérgicos. Por ejemplo en la discusión del experimento del electrón y la doble ranura, que es el modelo favorito de Bohr para ilustrar las novedosas características conceptuales de la Teoría Cuántica, y escribiendo al mismo tiempo sobre el EPR, Bohr argumenta lo siguiente.
Si sólo pudiésemos imaginar la posibilidad de que sin perturbar los fenómenos determinamos a través de qué agujero pasa el electrón, nos encontraríamos, verdaderamente, en un territorio irracional, para esto nos pondríamos en una situación en la cual un electrón, el cual podría decirse que pasa a través del agujero, estaría afectado por las circunstancias de si este [otro] agujero estaba abierto o cerrado; pero… es completamente incomprensible que en su último viaje [el electrón] se viese influenciado por si el agujero está abierto o cerrado. (Bohr 1935b)

Nótese lo cercano que se encuentra el lenguaje usado en los Sistemas Perturbativos al EPR. Pero aquí Bohr defiende la localidad y considera la contemplación de la no-localidad como “irracional” y “completamente incomprensible”. Dado que “la circunstancia de si este [otro] agujero estaba abierto o cerrado” afecta a los posibles tipos de predicciones considerando el futuro comportamiento del electrón, si extendemos el concepto de la “realidad” del electrón, como parece sugerir para el EPR, incluyendo tal información, “perturbamos” el electrón alrededor de un agujero abriendo o cerrando el otro. Esto es, si damos a la “perturbación” el mismo sentido que le aquí parece darle Bohr cuando responde a la EPR, entonces somos arrastrados a una no-localidad “incomprensible”, y pasamos al territorio de la irracional.

Existe otra forma de intentar comprender la posición de Bohr. De acuerdo con una lectura habitual (ver la Interpretación de Copenaghe), tras el EPR Bohr abrazó un informe de atribución de propiedad relacional (o contextual). En este informe hablar de la posición, es decir, de un sistema, presupone que ya se ha colocado en su lugar la interacción apropiada que involucra un aparato para medir la posición. De esta forma, la “posición” de un sistema se refiere a la relación entre el sistema y el dispositivo de medida. En el contexto del EPR esto parecería implicar que antes de que se mida la posición en el sistema de Albert, hablar de la posición del sistema de Niels está fuera de lugar; mientras que si se mide la posición del sistema de Albert, hablar de la posición del sistema de Niels es apropiado y, de hecho, podemos decir a ciencia ciertas que el sistema de Niels “tiene” una posición. Consideraciones similares gobiernan las medidas del momento. Se deduce, entonces, que las manipulaciones locales llevadas a cabo en el sistema de Albert, en un lugar que asumimos que no tiene relación que en sistema de Niels, puede afectar directamente, en un sentido lingüístico además de un hecho cierto, al sistema de Niels. De forma similar, en el montaje de la doble ranura, se aplicaría que lo que se puede decir de forma cierta sobre la posición del electrón alrededor del agujero superior dependería del contexto, si el agujero inferior está abierto o cerrado. Se podría sugerir que tales acciones relacionadas a distancia son inofensivas, tal vez meramente “semánticas”; como ser el “mejor” cuando tu único rival — que podría estar a kilómetros de distancia — falla. Aún así, plasman precisamente el tipo de no-localidad ya discutido con respecto a la “perturbación informativa”, y que Bohr parece aborrecer.

A la luz de todo esto es difícil saber qué respuesta fidedigna puede atribuirse a Bohr que desbarataría la EPR. Bohr bien podría haber sido consciente de la dificultad de enmarcar los conceptos apropiados con claridad cuando, unos años tras el EPR escribió:

Las desacostumbradas características de la situación con las que nos enfrentamos en la Teoría Cuántica precisan de la mayor cautela respecto a todas las cuestiones de terminología. Hablar como si a menudo se hiciera la perturbación de un fenómeno por la observación, o incluso de la creación de atributos físicos a objetos mediante procesos de medida es propenso a confundir, dado que todas las afirmaciones implican una partida desde convenciones del lenguaje básico que puede pensarse incluso que sean prácticos en pro de la brevedad, nunca pueden ser inequívocos (Bohr 1939, p. 320. Citado en la Sección 3.2 del Principio de Incertidumbre.)

3. Desarrollo del EPR

3.1 La versión de Bohm

Durante unos quince años tras su publicación, la paradoja EPR se discutió a nivel de un experimento de reflexión cuando las dificultades conceptuales de la Teoría Cuántica se convirtieron en la cuestión. En 1951 David Bohm, entonces Profesor Asistente sin cargo de la Universidad de Princeton y protegido de Robert Oppenheimer, publicó un libro de texto sobre la Teoría Cuántica en el cual profundiza en el EPR para desarrollar una respuesta en la línea de Bohr. Bohm demostró como se podría reflejar la situación conceptual en el experimento de reflexión del EPR observando la disociación de una molécula diatómica cuyo momento angular de espín total sea (y se mantenga) cero; por ejemplo, la disociación de una molécula de hidrógeno excitada en un par de átomos de hidrógeno a través de un proceso que no modifique un momento angular total inicial de cero (Bohm 1951, Secciones 22.15-22.18).En el experimento de Bohm los fragmentos atómicos se separan tras la interacción, volando libremente en distintas direcciones. Posteriormente, se hacen las medidas de sus componentes de espín (que aquí toman el lugar de la posición y momento), cuyos valores medidos serían anticorrelados tras la disociación. En el llamado estado individual del par atómico, el estado tras la disociación, si uno de los espines de los átomos se encuentra que es positivo con respecto a la orientación de un eje en ángulos adecuados a su ruta de vuelo, el otro átomo se encontraría que tiene un espín negativo con respecto a un eje de la misma orientación. Así como los operadores para posición y momento, los operadores de espín para distintas orientaciones no conmutan. Además, en el experimento esbozado por Bohm, los fragmentos atómicos pueden alejarse uno de otro y, por tanto, se convierten en objetos apropiados para las suposiciones que restringen los efectos de las acciones puramente locales. De esta forma, el experimento de Bohm refleja las correlaciones entrelazadas en la EPR para sistemas separados espacialmente, permitiendo argumentos y conclusiones similares que involucran localidad, separabilidad y completitud. Un artículo posterior, coescrito con Aharonov (Bohm y Aharonov 1957) pasa a describir la maquinaria para un experimento plausible en el cual estas correlaciones podrían verificarse. Se ha convertido en algo habitual referirse a las configuraciones experimentales que involucran determinaciones de las componentes espín para sistemas espacialmente separados, y a una variedad de configuraciones similares (especialmente unas para medida de polarización de fotones), como experimentos "EPRB" — "B" de Bohm. Sin embargo, debido a las dificultades técnicas de crear y monitorizar los fragmentos atómicos, parece que no hay intentos inmediatos de realizar una versión de Bohm de la EPR.

3.2 Bell y más allá

Así fue como se mantuvo la situación durante casi al menos otros quince años, hasta que John Bell usó la configuración EPRB para construir un asombroso argumento, cuando menos tan retador como la EPR, pero llegando a una conclusión distinta (Bell 1964). Bell demuestra que, bajo un conjunto de suposiciones dado, ciertas correlaciones que pueden medirse en las ejecuciones del experimento EPRB satisfacen un conjunto particular de restricciones, conocido como desigualdades de Bell. En estos experimentos EPRB, sin embargo, la Teoría Cuántica predice que las correlaciones medidas violan las desigualdades de Bell, y por una cantidad significativa experimentalmente. Así pues, Bell demuestra (ver la entrada del Teorema de Bell) que la Teoría Cuántica es inconsistente con las suposiciones dadas. Destacable entre estas es la suposición de localidad, similar a la suposición de localidad asumida tácitamente en la EPR y asumida explícitamente en las versiones de Einstein (excepto en el caso de la pólvora). De esta forma, el Teorema de Bell a menudo es caracterizado como una demostración de que la Teoría Cuántica es no-local. Sin embargo, dado que se necesitan otros supuestos en cualquier derivación de las desigualdades de Bell (aproximadamente, los supuestos garantizan una representación clásica de las probabilidades cuánticas; ver Fine 1982, y Malley 2004), se debería ser cauto al individualizar la localidad como algo necesariamente en conflicto con la Teoría Cuántica.

Los resultados de Bell fueron explorados y se profundizó en ellos gracias a distintas investigaciones teóricas y, a su vez, han estimulado un número cada vez mayor de delicados y sofisticados experimentos del tipo EPRB diseñados para probar si las desigualdades de Bell se mantienen cuando la Teoría Cuántica predice que deberían fallar. Con unas pocas excepciones anómalas, los experimentos confirman las violaciones cuánticas de las desigualdades. (Baggott 2004 contiene un recuento legible de los principales experimentos y refinamientos; pero lee Hess y Philipp 2004 para algunas reservas.) Las confirmación es cuantitativamente impresionante y, aunque existen aún caminos viables para reconciliar los resultados experimentales con los marcos de trabajo que abarcan la localidad y separabilidad (ver, por ejemplo., Larsson 1999, y Szabo y Fine 2002), se han hecho muchas conjeturas sobre que cuando se mejoren los experimentos, tales marcos de trabajo no soportarán la prueba del tiempo. Aunque el significado exacto de estas pruebas experimentales de las desigualdades de Bell hasta ahora se mantienen como una materia de continuada controversia, las técnicas desarrolladas en los experimentos, y las ideas teóricas relacionadas para usar el entrelazamiento asociado con las interacciones del tipo EPRB, se han convertido en algo importante por sí mismas. Estas técnicas e ideas, partiendo de la EPR y el Teorema de Bell, tienen aplicaciones hoy día que avanzan en varios campos de investigación relativamente nuevos — criptografía cuántica, teleportación y computación (ver Entrelazamiento Cuántico e Información).

Para volver al dilema de la EPR entre la localidad y completitud, parecería desde el Teorema de Bell que la estrategia de Einstein de mantener la localidad, y, de este modo, concluir que la descripción cuántica es incompleta, puede estar equivocada. Incluso aunque el Teorema de Bell no descarta de forma concluyente la localidad, se debería ser ciertamente cauteloso al suponerlo. Por otra parte, dado que el argumento de Einstein de la pólvora explosiva (o el gato de Schrödinger) apoyan la incompletitud sin suponer la localidad, se debería ser cauto al adoptar la otra parte del dilema, afirmando que las descripciones del estado cuántico son completas y “por tanto” que la teoría es no-local. Podría resultar que ambas partes tuviesen que ser rechazadas: las funciones de estado no proporcionan una descripción completa y la teoría es además no-local (aunque posiblemente aún separable; ver Winsberg y Fine 2003). Hay al menos una aproximación bien conocida a la Teoría Cuántica que hace una elección de este tipo, la aproximación de “de Broglie-Bohm” (Mecánicas Bohmianas). Por supuesto también puede ser posible romper el argumento EPR plausiblemente para el dilema cuestionando algunas de sus otras suposiciones (por ejemplo, separabilidad, el postulado de reducción, o el enlace eigenvalor-eigenestado). Esto llevaría a la opción que queda, considerar la teoría como ambas, local y completa. Si se hace convincente, tal vez alguna versión de la Interpretación de Everett vendrá a ocupar esta rama del árbol interpretativo.

Autor: Arthur Fine (Universidad de Washington)

Traductor: Manuel Hermán

Sitio Web: stanford.edu

Ir a la Primera Parte