Historia de las Matemáticas: El número Pi

Un versículo poco conocido de la Biblia dice: Hizo una fuente de metal fundido que medía 10 codos de diámetro: era completamente redonda, y su altura era de 5 codos y una línea de 30 codos lo rodeaba. (I Reyes 7, 23) El mismo versículo puede encontrarse en II Crónicas 4, 2. Aquí aparece en una lista de especificaciones para el gran templo de Salomón, construido sobre el 950 A.C. y su interés aquí radica en que da un valor de π = 3. No es un valor muy preciso, desde luego, e incluso no muy preciso para su época, lo egipcios y mesopotámicos habían dado valores de 25 / 8 = 3,125 y de √10 = 3,162 respectivamente en épocas mucho más recientes: aunque en defensa de los artesanos de Salomón debería hacerse notar que el elemento que se describe parece ser una pieza de metal fundida muy grande, donde un alto grado de precisión geométrica no es posible ni necesario. Hay algunas otras interpretaciones que llevan a un valor mucho más correcto. El hecho de que la razón de la circunferencia al diámetro de un círculo es constante ha sido conocido durante tanto tiempo que es casi imposible de rastrear. Los primeros valores para π que incluyen el valor “bíblico” de 3, fueron casi con certeza encontrados mediante medida. En el Papiro Egipcio de Rhind, que data del 1650 A.C, hay buenas pruebas para tomar 4 (8 / 9)2 = 3,16 como valor para π. El primer cálculo teórico parece haber sido llevado a cabo por Arquímedes de Siracusa (287-212 A.C.). Obtuvo la aproximación: 223 / 71 < π < 22 / 7. Antes de dar una indicación para su demostración, nota que existe un alto nivel de sofisticación en el uso de desigualdades. Arquímedes sabía, cosa que hoy desconoce mucha gente, que π no es igual a 22 / 7, y no hizo ninguna afirmación de haber descubierto el valor exacto. Si tomamos su mejor aproximación como la media de estos dos límites obtenemos 3,1418, un error de aproximadamente 0,0002. Aquí está el argumento de Arquímedes. Considera un círculo de radio 1, en el cual inscribimos un polígono regular de 3 x 2^n-1 lados, con un semiperímetro b_n, y superponemos un polígono regular de 3 x 2^n-1 lados, con un semiperímetro de a_n. El diagrama para el caso n = 2 está a la derecha. 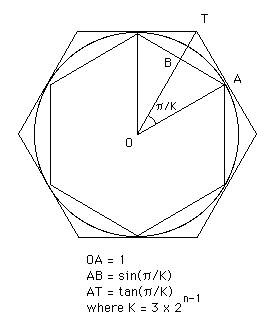El efecto de este procedimiento es definir una secuencia incremental: b₁ , b₂ , b₃ , ... y una secuencia decreciente a₁ , a₂ , a₃ , ... tales que ambas secuencias tienen como límite π. Usando notación trigonométrica, vemos que los dos semiperímetros vienen dados por a_n = K tan( π / K ), b_n = K sin( π / K ), donde K = 3 2n-1. Igualmente tenemos que a_n+1 = 2K tan( π / 2K), b_n+1 = 2K sin( π / 2K), y no es un complejo ejercicio de trigonometría demostrar que: 1 / a_n + 1 / b_n ) = 2 / a_n+1 . . . (1) a_n+1 b_n = (b_n+1 )² . . . (2) Arquímedes, comenzando desde a₁ = 3 tan( π / 3 ) = 3√3 and b₁ = 3 sin( π / 3 ) = 3√3/2, calculó a₂ usando (1), luego b₂ usando (2), a₃ usando (1), b₃ usando (2), y de esta forma hasta que calculó a₆ and b₆. Su conclusión fue que b₆ < π < _a . Es importante darse cuenta de que el uso de la trigonometría aquí no es histórico: Arquímedes no tenía las ventajas de una notación algebraica y trigonométrica y tuvo que derivar (1) y (2) de forma puramente geométrica. Además no tuvo siquiera la ventaja de nuestra notación decimal para los números, por lo que el cálculo de a₆ and b₆ a partir de (1) y (2) no fue de ninguna forma una tarea trivial. Por tanto fue una fabulosa proeza de imaginación y cálculo y la maravilla no es que parase en polígonos de 96 lados, sino que fue más lejos. Por supuesto, no hay razón en principio por la que no se debería continuar. Distinas personas lo hicieron, incluyendo a:

Nombre	Año	Precisión
Ptolomeo	150 A.C	3,1416
Zu Chongzhi	430-501 A.C	355 / 113
al-Khwarizmi	800	3,1416
al-Kashi	1430	14 dígitos
Viète	1540-1603	9 posiciones
Roomen	1561-1615	17 posiciones
Van Ceulen	1600	17 posiciones

Excepto para Zu Chongzhi, sobre quién no sabemos prácticamente nada y que es muy improbable que conociese el trabajo de Arquímedes, no se produjo ningún avance teórico en estas mejoras, solo mayor energía en el cálculo. Nota como la cabecera, es todos estas materias científicas, pasaron de Europa al Este desde el milenio que va del 400 al 1400 D.C. Al-Khwarizmi vivió en Bagdad, y dio su nombre a “algoritmo”, mientras que las palabrasal jabr en el título de uno de sus libros nos dio la palabra “álgebra”. Al-Kashi vivió incluso más al Este, en Samarkanda, mientras que Zu Chongzhi, no es necesario añadir, vivió en China. El Renacimiento europeo ocasionó en su debido momento todo un nuevo mundo matemático. Entre los primeros efectos de este redespertar fue la aparición de fórmulas matemáticas para π. Una de las primeras fue la de Wallis (1616-1703): 2 / π = (1.3.3.5.5.7. ...) / (2.2.4.4.6.6. ...) y una de las más conocidas es: π / 4 = 1 – 1 / 3 + 1 / 5 – 1 / 7 + .... Esta fórmula se le atribuye en muchos casos a Leibniz (1646-1716) pero parece que fue descubierta en primer lugar por James Gregory (1638- 1675). Estas son dos espectaculares y asombrosas fórmulas, ya que las expresiones de la derecha son de carácter completamente aritmético, mientras π emerge en primera instancia de la geometría. Demostraron los sorprendentes resultados que los procesos infinitos pueden lograr y muestran el camino a la maravillosa riqueza de la matemática moderna. Desde el punto de vista del cálculo de π, sin embargo, no tenía ningún uso. En las series de Gregory, por ejemplo, para obtener un resultado con 4 posiciones decimales correctas se requiere que el error sea menor que 0,00005 =1 / 20 000, y para esto necesitamos unos 10 000 términos de la serie. Sin embargo, Gregory también demostró el resultado más general tan^-1 x = x – x³ / 3 + x⁵ / 5 - ... (-1 ≤ x ≤ 1) . . . (3) a partir del cual obtenemos la primera serie si tomamos x = 1. Por lo que usando el hecho de que tan^-1( 1 / √3 ) = π / 6 tenemos que π / 6 = ( 1 / √3 )( 1 – 1 / (3.3) + 1 / (5.3.3) – 1 / (7.3.3.3) + ... la cual converge mucho más rápidamente. El décimo término es 1 / (19 x 3⁹√3), lo cual es menos que 0,00005, y por tanto al menos 4 decimales correctos tras solo 9 términos. Una idea incluso mejor es tomar la fórmula: π / 4 = tan^-1( 1 / 2 ) + tan^-1( 1 / 3 ) . . . (4) Y entonces resultan las dos series obtenidas poniendo primero 1 / 2 y 1 / 3 dentro (3). Claramente tendremos una convergencia muy rápida, en efecto, si podemos encontrar una fórmula similar a esta: π / 4 = tan^-1( 1 / a ) + tan^-1( 1 / b ) Con a y b graneds. En 1706 Machin encontró tal fórmula: π / 4 = 4 tan^-1( 1 / 5 ) – tan^-1( 1 / 239 ) . . . (5) En realidad esto no es difícil de probar, si sabes cómo demostrar (4) entonces no hay ninguna dificultad extra en (5), excepto que la aritmética es más compleja. Imaginar esto en primer lugar, por supuesto, es un tema bastante distinto. Con una fórmula como esta disponible, la única dificultad en calcular π es superar el aburrimiento del cálculo continuo. Ni que decir tiene que algunas personas fueron lo bastante estúpidas como para dedicar ingentes cantidades de tiempo y esfuerzo en este tedioso y completamente inútil pasatiempo. Uno de ellos, un inglés llamado Shanks, usó la fórmula de Machin para calcular 707 lugares de π, publicando los resultados de muchos años de trabajo en 1873. Shanks ha conseguido la inmortalidad por una razón muy curiosa que explicaremos en un momento. Aquí tenemos un resumen de cómo se produjeron las mejoras:

• 1699: Sharp usó el cálculo de Gregory para obtener 71 dígitos correctos
• 1701: Machin usó una mejora para obtener 100 dígitos. Los siguientes usaron sus métodos
• 1719: de Lagny encontró 112 dígitos correctos
• 1789: Vega obtuvo 126 lugares y en 1794 obtuvo 136
• 1841: Rutherford calculó 152 dígitos y en 1853 obtuvo 440
• 1873: Shanks calculó 707 posiciones de las cuales 527 eran correctas

Está disponible una cronología más detallada. Shanks sabía que π era irracional dado que había sido demostrado en 1761 por Lambert. Poco después del cálculo de Shanks se demostró por parte de Lindemann que π es transcendental, esto es, π no es la solución de ninguna ecuación polinómica con coeficientes enteros. De hecho este resultado de Lindemann demostró que la “cuadratura del círculo” era imposible. La trascendencia de π implica que no hay regla ni compás que permitan construir un cuadrado con un área igual a un círculo dado. Justo tras los resultados de Shanks De Morgan informó de una rareza estadística curiosa, que encontró que en los últimos 707 dígitos había una sospechosa carencia de sietes. Menciona esto en su Budget of Paradoxes de 1872 y la curiosidad permaneció hasta que en 1945 Ferguson descubrió que Shanks había cometido un error en la posición 528, tras la cual todos sus dígitos eran incorrectos. En 1949 se usó un ordenador para calcular 2000 posiciones de π. En esta y todas las siguientes expansiones por ordenador el número de sietes no difiere significativamente de lo esperado, y efectivamente la secuencia de dígitos ha pasado hasta ahora todos los test estadísticos de aleatoriedad. Deberíamos comentar algo sobre cómo surgió la notación de π. Oughtred en 1647 usó el símbolo d / π para la razón del diámetro de un círculo a su circunferencia. David Gregory (1697) usó π / r para la razón de la circunferencia de un círculo a su radio. El primer uso de π con su significado actual se debe al matemático galés William Jones en 1706 cuando afirmó "3,14159 andc. = π". Euler adoptó el símbolo en 1737 y rápidamente se convirtió en una notación estándar. Concluimos con una curiosidad estadísticas más sobre el cálculo de π, llamado el experimento de la aguja de Buffon. Si tenemos una rejilla uniforme de líneas paralelas, con una separación de distancia unitaria y lanzamos una aguja de longitud k < 1 en la rejilla, la probabilidad de que la aguja crece una línea es de 2k / π. Distintas personas han intentado calcular π arrojando agujas. El resultado más notable fue el de Lazzerini (1901), quien hizo 34 080 lanzamiento y obtuvo: π = 355 / 113 = 3.1415929 lo cual, es de hecho, el valor encontrado por Zu Chongzhi. Este resultado es sospechosamente bueno, y el truco lo revela el extraño número de 34 080 lanzamientos. Kendall y Moran comentan que un buen valor puede obtenerse deteniendo el experimento en un momento óptimo. Si estableces de antemano el número de lanzamientos que deben hacerse entonces tienes una forma muy imprecisa de calcular π. Kendall y Moran comentan que sería mejor cortar un gran círculo de madera y unas una cinta de medida para encontrar su circunferencia y diámetro. Siguiendo con el tema de los experimentos falsos Gridgeman, en un artículo que desdeñaba a Lazzerini y otros, provocó bastantes risas usando una aguja de una longitud cuidadosamente escogida de k = 0,7857, arrojándola dos veces, y consiguiendo que cruzara la línea en una de ellas. Así pues su estimación de π estaba dada por: 2 x 0,7857 / π = 1 / 2 a partir de lo cual tenemos el encomiable valor de π = 3,1428. ¡No lo hizo en serio! Es casi increíble que una definición de π fuese usada, al menos como excusa, para un ataque racial sobre el eminente matemático Edmund Landau en 1934. Landau había definido π en su libro de texto publicado en Göttingen en aquel año usando el, ahora bastante usual, método de decir que π / 2 es el valor de x entre 1 y 2 para el cual el coseno de x es cero. Esto desató una disputa académica que terminó con la destitución de Landau de su puesto en Göttingen. Bieberbach, un eminente teórico numérico que hacía el ridículo con sus visiones racistas, explicó las razones para la destitución de Landau:- De esta forma el valiente rechazo por el cuerpo de estudiantes de Göttingen que un gran matemático, Edmund Landau, ha experimentado es debido en un análisis final al hecho de que el estilo no-germano de este hombre en sus enseñanzas e investigaciones es insostenible con los sentimientos germanos. Una gente que ha observado como miembros de otras razas están trabajando para imponer ideas extranjeras a sí mismos debe rechazar profesores de una cultura ajena. G H Hardy replicó inmediatamente a Bieberbach en una nota publicada acerca de los consecuencias de esta definición no-germana de π: Hay muchos de nosotros, ingleses y alemanes, que dijimos durante la Guerra cosas [N del T: Se sobreentiende la Primera Guerra Mundial] sin sentido y que ahora lamentamos recordar. La ansiedad por la propia posición, el miedo a caer tras el creciente torrente de estupideces, la determinación a todo coste de no quedar al descubierto, pueden ser naturales, si no particularmente heroicas, excusas. La reputación del Profesor Bieberbach excluye tales explicaciones a sus palabras, lo que me lleva a la poco caritativa conclusión de que realmente cree que tiene razón. No solo los alemanes tuvieron en la actualidad problemas con π. En los Estados Unidos el valor de π dio lugar a un acalorado debate político. En el Estado de de Indiana en 1897 la Cámara de Representantes aprobó por unanimidad una Proyecto de Ley introduciendo una nueva verdad matemática. Promulgado por la Asamblea del Estado de Indiana: Se ha encontrado que el área de un círculo es el cuadrado de una línea igual al cuadrante de la circunferencia, así comoel área de un rectángulo equilátero es el cuadrado de uno de los lados. (Sección I, House Bill No. 246, 1897) El Senado de Indiana se mostró un poco más sensato y ¡pospuso de forma indefinida la adopción del decreto! Cuestiones abiertas sobre el número π

• ¿Cada uno de los dígitos 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 aparecen infinitamente con frecuencia en π?
• Cuestión de Brouwer: En la expansión decimal de π, ¿hay alguna posición donde mil dígitos consecutivos sean todos cero?
• ¿En π simplemente normal en base 10? ¿Hace esto que cada dígito aparezca con la misma frecuencia en su expansión decimal en un sentido asintótico?
• ¿Es π normal en base 10? ¿Hace esto que cada bloque de dígitos de una longitud dada aparezca con la misma freciencia en su expansión decimal en un sentido asintótico?
• ¿Es π normal? ¿Hace esto que cada bloque de dígitos de una longitud dada aparezca con la misma frecuencia en la expansión de cada base en un sentido asintótico? El concepto fue introducido por Borel en 1909.
• ¡Otra cuestión normal! Sabemos que π no es un número racional ya que no hay ningún punto a partir del cual sus dígitos comiencen a repetirse. Sin embargo, si π es normal entonces el primer millón de dígitos 314159265358979... tendrá lugar desde algún punto. ¡Incluso si π no es normal esto se matiene! ¿Es así? ¿Si es así, desde qué punto? Nota: Por encima de 200 millones lo más largo en aparecer es 31415926 y aparece dos veces.

Como posdata, aquí tienes una regla mnemotécnica para la expansión decimal de π. Cada dígito es el número de letras de la palabra correspondiente. How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics. All of thy geometry, Herr Planck, is fairly hard...: 3.14159265358979323846264... Traducción de la regla: [Cómo deseo beber, alcohol por supuesto, tras las pesadas lecturas sobre la mecánica cuántica. Toda su geometría, Señor Planck, es bastante dura...] Autores: J J O'Connor and E F Robertson MacTutor History of Mathematics Artículos Relacionados: Historia de las Matemáticas: El Cero Historia de las Matemáticas: El Infinito Bibliografía: 1. A Ahmad, On the π of Aryabhata I, Ganita Bharati 3 (3-4) (1981), 83-85. 2. L Badger, Lazzarini's lucky approximation of π, Math. Mag. 67 (2) (1994), 83-91. 3. P Beckmann, A history of π (Boulder, Colo., 1971). 4. E M Bruins, With roots towards Aryabhata's π-value, Ganita Bharati 5 (1-4) (1983), 1-7. 5. G L Cohen and A G Shannon, John Ward's method for the calculation of pi, Historia Mathematica 8 (2) (1981), 133-144. 6. P Freguglia, The determination of π in Fibonacci's 'Practica geometriae' in a fifteenth-century manuscript (Italian), Contributions to the history of mathematics (Italian) (Modena, 1990), 75-84. 7. N T Gridgeman, Geometric probability and the number π, Scripta Math. 25 (1960), 183-195. 8. R C Gupta, The value of π in the 'Mahabharata', Ganita Bharati 12 (1-2) (1990), 45-47. 9. R C Gupta, On the values of π from the Bible, Ganita Bharati 10 (1-4) (1988), 51-58. 10. R C Gupta, New Indian values of π from the 'Manava'sulba sutra', Centaurus 31 (2) (1988), 114-125. 11. R C Gupta, Lindemann's discovery of the transcendence of π : a centenary tribute, Ganita Bharati 4 (3-4) (1982), 102-108. 12. R C Gupta, Some ancient values of pi and their use in India, Math. Education 9 (1975), B1-B5. 13. R C Gupta, Madhava's and other medieval Indian values of pi, Math. Education 9 (3) (1975), B45-B48. 14. R C Gupta, Aryabhata I's value of π, Math. Education 7 (1973), B17-B20. 15. T Hayashi, T Kusuba and M Yano, Indian values for π derived from Aryabhata's value, Historia Sci. 37 (1989), 1-16. 16. E W Hobson, Squaring the circle (London, 1953). 17. C Jami, Une histoire chinoise du 'nombre π', Archive for History of Exact Sciences 38 (1) (1988), 39-50. 18. S K Jha, and M Jha, A study of the value of π known to ancient Hindu and Jaina mathematicians, J. Bihar Math. Soc. 13 (1990), 38-44. 19. P Jha, Aryabhata I and the value of π, Math. Ed. (Siwan) 16 (3) (1982), 54-59. 20. R P Kulkarni, The value of π known to Sulbasutrakaras, Indian J. Hist. Sci. 13 (1) (1978), 32-41. 21. K Nakamura, On the sprout and setback of the concept of mathematical "proof" in the Edo period in Japan : regarding the method of calculating number π, Historia Sci. (2) 3 (3) (1994), 185-199. 22. C T Rajagopal and T V Vedamurti Aiyar, A Hindu approximation to pi, Scripta Math. 18 (1952), 25-30. 23. R Roy, The discovery of the series formula for π by Leibniz, Gregory and Nilakantha, Math. Mag. 63 (5) (1990), 291-306. 24. C Pereira da Silva, A brief history of the number π (Portuguese), Bol. Soc. Paran. Mat. (2) 7 (1) (1986), 1-8. 25. D Singmaster, The legal values of pi, Math. Intelligencer 7 (2) (1985), 69-72. 26. M D Stern, A remarkable approximation to π, Math. Gaz. 69 (449) (1985), 218-219. 27. P E Trier, Pi revisited, Bull. Inst. Math. Appl. 25 (3-4) (1989), 74-77. 28. I Tweddle, John Machin and Robert Simson on inverse-tangent series for π, Archive for History of Exact Sciences 42 (1) (1991), 1-14. 29. A Volkov, Calculation of π in ancient China : from Liu Hui to Zu Chongzhi, Historia Sci. (2) 4 (2) (1994), 139-157. 30. Y-L Zha, Research on Tsu Ch'ung-Chih's approximate method for π, in Science and technology in Chinese civilization (Teaneck, NJ, 1987), 77-85.