Historia de la ciencia»Las matemáticas en los papiros egipcios
Las matemáticas en los papiros egipcios
Publicado por J J O'Connor y E F Robertson | 22/06/2009En este artículo vamos a echar una mirada detallada a las matemáticas que contienen los papiros egipcios sobrevivientes más importantes.

En el artículo las matemáticas egipcias vimos algunos detalles de los papiros egipcios sobrevivientes más importantes. En este artículo vamos a echar una mirada detallada a las matemáticas que contienen.
Ahmes, en el papiro Rhind, ilustra el método egipcio de multiplicación de la siguiente manera: Supongamos que se quiere multiplicar 41 por 59. Toma 59 y sumárselo a sí mismo, después suma la respuesta a sí misma y continúa:
41 59
_________________
1 59
2 118
4 236
8 472
16 944
32 1888
41 - 32 = 9, 9 - 8 = 1, 1 - 1 = 0Ya que 64 > 41, no hay necesidad de ir más allá de la entrada 32. Ahora hay que hacer una serie de restas para ver que 41 = 32 + 8 + 1. Después hay que verificar los números en la columna derecha que correspondan a 32, 8 y 1 y sumarlos.
41 59
_________________
1 59
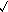
2 118
4 236
8 472
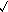
16 944
32 1888
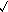
_________________
2419
Nótese que la multiplicación se consigue sumando solamente; nótese también que este es un uso muy temprano de la aritmética binaria (ver abajo). Invirtiendo los factores tenemos:
59 41
_________________
1 41
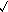
2 82
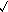
4 164
8 328
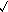
16 656
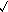
32 1312
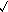
_________________
2419
Nótese que para que este método funcione, se necesita saber que cada número es la suma de dos potencias de 2. Los antiguos egipcios no habrían tenido una demostración de esto ni habrían sentido que tal demostración fuera necesaria. Simplemente habrían sabido a partir de la experiencia que siempre podía hacerse así. Básicamente podemos pensar en este método como escribir uno de los números en base dos. En los ejemplos anteriores hemos escrito
41 = 1×20 + 0×21 + 0×22 + 1×23 + 0×24 + 1×25
y
59 = 1×20 + 1×21 + 0×22 + 1×23 + 1×24 + 1×25
La división también funciona multiplicando por dos. Por ejemplo, para dividir 1495 por 65 se prosigue así:
| 1 | 65 |
| 2 | 130 |
| 4 | 260 |
| 8 | 520 |
| 16 | 1040 |
Nos detenemos en este punto ya si duplicamos el último número, llegaríamos a uno mayor a 1495. Ahora buscamos los números en la columna derecha que suman 1495. Vemos que 1040 + 260 + 130 + 65 = 1495 y marcamos los renglones correspondientes:
| 1 | 65 | 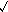 |
| 2 | 130 | 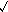 |
| 4 | 260 | 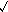 |
| 8 | 520 | |
| 16 | 1040 | 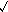 |
Ahora sumamos los números de la columna izquierda que están en los renglones marcados:
16 + 4 + 2 + 1 = 23,
por lo que 1495 dividido entre 65 da 23. ¿Qué pasa si la división no es exacta? En ese caso el método egipcio dará fracciones como muestra el siguiente ejemplo. Para dividir 1500 entre 65, hay que proceder como antes:
| 1 | 65 |
| 2 | 130 |
| 4 | 260 |
| 8 | 520 |
| 16 | 1040 |
Nuevamente, nos detenemos aquí ya que el siguiente número es mayor a 1500. Ahora hay que buscar los números en la columna derecha que sumen a un número n tal que 1500 - 65 < n ≤ 1500 [Los egipcios sabían que hacer esto era posible siempre. ¿Puedes probar que es cierto?]. En este caso tenemos que
1040 + 260 + 130 + 65 = 1495
y estamos a 5 de la suma buscada. Otra vez hay que marcar los renglones correspondientes a estos números:
| 1 | 65 | 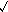 |
| 2 | 130 | 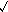 |
| 4 | 260 | 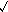 |
| 8 | 520 | |
| 16 | 1040 | 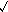 |
Ahora hay que sumar los números de la izquierda de las columnas marcadas:
16 + 4 + 2 + 1 = 23,
así que 1500 dividido por 65 da 23 y sobran 5/65 = 1/13. Por lo tanto, la respuesta es 23 + 1/13. Hemos hecho una pequeña trampa aquí ya que la fracción obtenida es una fracción unitaria, es decir, un número racional de la forma 1/n, con n entero. De hecho, los egipcios solamente tenían fracciones de este tipo y si la respuesta no hubiera involucrado una fracción unitaria, entonces los egipcios hubieran escrito la parte fraccionaria como la suma de fracciones unitarias. Más adelante veremos cómo se hacía esto al examinar un caso más general. El siguiente problema es cómo multiplicar y dividir números que involucran fracciones. El primer punto a destacar es que los egipcios usaban únicamente fracciones unitarias y, para poder calcular una tabla, se necesitaba convertir dos veces una fracción unitaria en una suma de fracciones unitarias. Ahora bien, podría pensarse que duplicar la fracción unitaria 1/5 sería fácil y produciría la suma de las fracciones unitarias 1/5 + 1/5. Sin embargo, por razones que comprendemos totalmente, este no fue su acercamiento. Ellos escribían el doble de una fracción unitaria como la suma de dos fracciones unitarias distintas. Por ejemplo, el doble de 1/5 se escribiría 1/3 + 1/15. El papiro de Rhind da una tabla para duplicar fracciones unitarias 1/n para n impar, n entre 5 y 101. Hay que notar que Ahmes no necesitó dar el doble de 1/n para n para, ya que ésta es simplemente 1/m, donde m = 2n. La tabla de duplicación de las fracciones unitarias empieza
Es sorprendente que no haya errores en la tabla. Ciertamente Ahmes habría sido un experto para calcular y este no habría sido simplemente un ejercicio de copia para él. Hay unos cuantos errores en el papiro Rhind pero los que hay parecen ser errores de cálculo, no de copia ya que el resultado incorrecto se usa más adelante en vez de regresar al camino correcto como sucedería con un error cometido al copiar. También está la fascinante pregunta de cómo se encontraron estas descomposiciones y de por qué se escogieron estas en particular en vez de otras. Esto se discute en [6] y otras ideas que añaden y corrigen la información en [6] se dan en [17], [18], [29] y [35]. Las reglas favoritas que muchos historiadores como Gillings creen que guiaban a los escribas al elegir la descomposición de 2/n en fracciones unitarias son (1) preferir números pequeños, (2) cuantos menos términos, mejor; y nunca usar más de cuatro (3) preferir los números pares que los impares. Sin embargo otros historiadores, por ejemplo Bruins, argumentan contra estas reglas. Afirman esencialmente que antes de aplicar estas reglas se necesitaría encontrar todas las descomposiciones unitarias de 2/n y no hay evidencia de que los egipcios tuvieran algún método para poder hacerlo. Para dar un ejemplo de cómo usar la tabla, examinemos el Problema 21 del papiro Rhind. Nótese que 2/3 era para los egipcios una fracción aceptable a pesar de no ser unitaria. Problema 21: Completar 2/3 y 1/15 para obtener 1. En términos modernos, lo que se pide es una fracción x tal que
2/3 + 1/15 + x = 1.
El método de solución consistía en 'deshacerse' de las fracciones por medio de una multiplicación. En este caso, multiplicando cada una por 15 se obtiene
10 + 1 + y = 15.
A ésta se le llama ecuación 'auxiliar roja' ya que el escriba la anotaba con tineta roja (claro que no aparecería en esta forma sino como 'completar 10 y 1 a 15'). La solución a la ecuación auxiliar roja es 4 así que la solución de la ecuación original sería doble × (doble × 1/15). De la tabla de dobles vemos que la fracción doble de 1/15 es 1/10 + 1/30. Duplicar esto da 1/5 + 1/15 que es la solución al Problema 21. Otro ejemplo de cómo resolver una ecuación está dado en el Problema 24, el cual pregunta: Problema 24: Se añade una cantidad a un cuarto de esa cantidad y se obtiene 15. ¿Cuál es la cantidad? Ahmes usa el 'método' de la posición falsa', que era un procedimiento estándar aún tres mil años después. En notación moderna el problema consiste en resolver
x + x/4 = 15.
Ahmes supone la respuesta x = 4. Esto es quitar la fracción en el término x/4. Ahora, con x = 4, la expresión x + x/4 se convierte en 5. Ésta no es a respuesta correcta, ya que la expresión debe ser igual a 15. Sin embargo, 15 es 3 veces 5 así que tomando 3 veces la respuesta inicial x = 4, es decir, x = 12, le da a Ahmes el resultado correcto. Otra interpretación, favorecida por algunos historiadores, es que Ahmes pensaba en el método como dividir x en 4 piezas iguales cuyo tamaño había que determinar. Entonces Ahmes calcula x + x/4 obteniendo 5 de esas piezas iguales. Cada pieza debe ahora valer tres de forma que 5 piezas sean igual a 15. Esto no es muy distinto de a forma previa de pensar pero es posible que se parezca más a la manera de pensar de Ahmes. Finalmente, Ahmes verifica su solución, o demuestra que su respuesta es correcta. Toma x = 4 × 3 = 12. Entonces x/4 = 3 y, por lo tanto, x + x/4 = 15 como se requería. El método de posición falsa se usa en los Problemas 24 al 29 del papiro Rhind. Sin embargo, en el Problema 31, Ahmes usa el método más sencillo de división pura. Esto se aborda en detalle en [31]. Veamos ahora cómo multiplicar, usando métodos egipcios, 1 + 1/3 + 1/5 entre 30 + 1/3.
| 1 | 1 + 1/3 + 1/5 |
| 2 | 2 + 2/3 + 1/3 + 1/15 = 3 + 1/15 |
| 4 | 6 + 1/10 + 1/30 |
| 8 | 12 + 1/5 + 1/15 |
| 16 | 24 + 1/3 + 1/15 + 1/10 + 1/30 |
| 2/3 | 2/3 + 1/6 + 1/18 + 1/10 + 1/30 |
| 1/3 | 1/3 + 1/12 + 1/36 + 1/20 + 1/60 |
Aquí, el renglón que empieza con 2/3 se ha calculado como 2/3 de 1 es 2/3, 2/3 de 1/3 es el doble de 1/9 que es 1/6 + 1/18, 2/3 de 1/5 que es 1/10 + 1/30. A continuación hay que encontrar los números de la columna izquierda que sumen 30 + 1/3. Estos están en las columnas señaladas:
| 1 | 1 + 1/3 + 1/5 | |
| 2 | 3 + 1/15 | 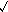 |
| 4 | 6 + 1/10 + 1/30 | 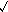 |
| 8 | 12 + 1/5 + 1/15 | 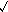 |
| 16 | 24 + 1/3 + 1/15 + 1/10 + 1/30 | 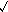 |
| 2/3 | 2/3 + 1/6 + 1/18 + 1/10 + 1/30 | |
| 1/3 | 1/3 + 1/12 + 1/36 + 1/20 + 1/60 |  |
Al sumar las entradas de la columna derecha de los renglones señalados, se obtiene el resultado de la multiplicación
46 + 1/5 + 1/10 + 1/12 + 1/15 + 1/30 + 1/36.
Dando una última mirada al papiro Rhind, damos la solución al Problema 50. Un campo circular tiene un diámetro de 9 khetii. ¿Cuál es su área? Aquí está la solución dada por Ahmes. Restar 1/9 del diámetro, es decir 1; el residuo es 8. Multiplicar 8 veces 8; da 64. Por lo tanto, contiene 64 setatiii de tierra. Se hace así:
| 1 | 9 |
| 1/9 | 1 |
al quitárselo, quedan 8
| 1 | 8 |
| 2 | 16 |
| 4 | 32 |
| 8 | 64 |
El área es 64 setat. Hay que señalar que la solución es equivalente a tomar π = 4(8/9)2 = 3.1605. Este es un resultado notable si tomamos en cuenta la fecha en la que esta aproximación debe haber sido descubierta. La pregunta fascinante que se plantea es cómo pudo haberse hecho este descubrimiento. Aunque no tenemos manera de llegar a saberlo con certeza, se han sugerido diversas conjeturas. En [25], Gerdes da tres ideas que podrían haber llevado a los egipcios a este resultado. Dos de las conjeturas sugeridas en [25] se refieren a artesanías africanas en las que muchas veces se encuentran una curva serpentina y un conjunto de anillos concéntricos equidistantes. Estos dos diseños geométricos están esparcidos por toda África y Gerdes muestra cómo estos podrían haber llevado a una fórmula para el área del círculo. La tercera conjetura en [25] se refiere a un juego de mesa, 'mancala', que era popular por toda África y el antiguo Egipto. El juego involucra comparar círculos pequeños con grandes y puede haber proporcionado la motivación para la fórmula del área. #3#Aunque los métodos matemáticos que hemos descrito se encuentran en varios documentos egipcios, todos los ejemplos que hemos dado hasta aquí vienen del papiro Rhind. Terminemos el artículo con un ejemplo del papiro de Moscú, sobre el cual muchos historiadores afirman que es el logro más impresionante de las matemáticas egipcias. Se trata del problema 14 del papiro e involucra a la figura geométrica que puede verse en el pedazo del papiro de Moscú en la imagen a la derecha. Ejemplo 14. Ejemplo del cálculo de una pirámide truncada. La base es un cuadrado que mide 4 codosi por lado, la tapa es un cuadrado cuyos lados miden 2 codos y la altura de la pirámide truncada es de 6 codos. En primer lugar debemos señalar que por 'calcular la pirámide', el autor quiere decir 'calcular el volumen de la pirámide'. En segundo lugar, notar qué tan apropiado es este cálculo para la civilización que hoy es universalmente famosa por su notable construcción de pirámides. El cálculo inicia por determinar el área de la base: 4×4 = 16. Entonces se encuentra el área de la tapa: 2×2 = 4. Después se computa el producto del lado de la base por el lado de la tapa: 4×2 = 8. Estos números se suman: 16 + 4 + 8 = 28. Ahora se toma 1/<sub3 de la altura, es decir, 2. Finalmente se toman el producto de 1/<sub3 de la altura con la suma previa de 28 y el escriba anota:
Miren que da 56
Este ejemplo indica que el egipcio conocía la fórmula del volumen (aunque, claro, no en el sentido algebraico en el que nosotros pensamos en las fórmulas). Si cada lado de la base cuadrada mide a, cada lado de la tapa cuadrada b y la altura es h, entonces
V = h (a2 + ab + b2)/3.
Artículo de: J J O'Connor y E F Robertson
Notas
- La principal unidad de medida de los antiguos egipcios era el 'codo', equivalente a 52.3cm Ver Matemáticas en Egipto: medida
- El 'khet' era un múltiplo del codo equivalente a 100 codos reales, equivalentes a 52,3 m
- El 'setat' es la unidad fundamental de superficie equivalente a un cuadrado de 1 'khet' de lado, equivalía aproximadamente a un cuadrado de tierra de unos 52 metros de lado.
- Twittear
- » Que es la materia?Por Jaime Rudas | 48 comentarios
- » Carrera contrarreloj para detectar materia oscuraPor Valer | 16 comentarios
- » Viajes interestelaresPor eferreyra | 45 comentarios
- » INSTANTE ETERNOPor Avicarlos | 12 comentarios
- » Sonda Dawn a Vesta y CeresPor eferreyra | 96 comentarios
- » creando un alien a partir de su entornoPor aregidor | 50 comentarios
- » ¿Qué nos sugieren los exoplanetas sobre el Sistema Solar?Por Raul | 11 comentarios
- » Larga vida y prosperidadPor Raul | 3 comentarios
- » Inclinación sistemas planetarios respecto plano galácticoPor tedibear | 2 comentarios
- » El arcaPor Jaime Rudas | 5 comentarios



Comentarios