Estás viendo Biografías

Biografía de Maurits Cornelius Escher

Publicado por Covadonga Escandón Martínez | 06/02/2025

Artículo histórico de Astroseti, recuperado y revisado por Xavier Civit

Nacido: 17 de junio de 1898 en Leeuwarden, Holanda Fallecido: 27 de marzo de 1972 en Laren, Holanda

Maurits Escher, sus padres siempre lo llamaron Mauk. Fue criado por su padre, George Escher, ingeniero civil, y su segunda esposa Sarah quien era hija de un ministro gubernamental. Vivía con sus cuatro hermanos mayores, Arnold, Johan, Berend y Edmond. Maurits asistía tanto a la escuela primaria como al bachillerato en Arnhem entre 1912 y 1918 donde no brilló en muchas materias pero mostraba un interés temprano tanto por la música como por la carpintería. Se opinaba que poseía una mente matemática pero nunca sobresalió en la materia durante sus años escolares y la trataba con considerable desasosiego. Escribía:

Durante el bachillerato en Arhhem salí muy mal en aritmética y álgebra porque tenía, y aún tengo, gran dificultad con la abstracción de números y letras. Cuando, más adelante, en estereometría [geometría de los sólidos], se apeló a mi imaginación, las cosas mejoraron un poco pero en la escuela nunca salí bien en esa materia. Pero nuestro camino por la vida puede dar giros extraños.

Hay informes que detallan su acercamiento metodológico a la vida, que se considera como una reacción inconsciente a su educación en una familia de ingenieros. Como niño, Mauricio siempre tuvo un lado intensamente creativo y una "aguda capacidad de asombro". Muchas veces decía ver formas en las nubes con las cuales se identificaba. Maurits y su buen amigo Bas Kilt se interesaron mucho en las técnicas de impresión después de recibir buenas notas de sus departamentos de arte respectivos, los cuales habían motivado a estos alumnos a experimentar. Las intenciones familiares de que Maurits se entrenara como arquitecto quedaron anuladas cuando no aprobó sus exámenes finales de historia, organizaciones constitucionales, economía política y contabilidad; por ello nunca se graduó oficialmente. Su familia se mudó a Oosterbeek donde un agujero en la ley holandesa permitía que Maurits se inscribiera en la Escuela Superior Técnica en Delft (1918-1919) y así podía repetir algunas de las materias que había reprobado. Incapaz y poco dispuesto a ponerse al corriente después de estar enfermo, Maurits decidió concentrarse en sus dibujos y sus técnicas de grabado en madera. Fue influenciado y entrenado inicialmente por R. N. Roland Holst:

Me sugirió insistentemente que hiciera algunos grabados en madera y lo hice de inmediato [...] Es un trabajo maravilloso pero bastante más difícil que trabajar con linóleo.

En septiembre de 1920 Maurits se muda a Haarlem en un último intento de cumplir el deseo de su padre de que estudiara arquitectura y se matriculó en la Escuela de Arquitectura y Artes Decorativas. Un encuentro casual con Samuel Jesserum de Mesquita, un profesor de artes gráficas, sería un punto destacado en la vida de Escher quien quedó convencido de que un programa de artes gráficas sería lo más adecuado para sus habilidades. De Mesquita le enseñó al entusiasta Escher todo lo que sabía sobre técnicas de xilografía, le dejó experimentar y lo animó a hacerlo ampliamente para que desarrollara sus habilidades. Escher se quejaba regularmente de su falta de habilidad natural para dibujar y como resultado le tomaba mucho tiempo terminar la mayor parte de sus piezas y necesitaba de varios intentos antes de quedar totalmente satisfecho. En su juventud se concentró en los paisajes, muchos de los cuales eran dibujados desde perspectivas inusuales. También hizo numerosos bocetos de plantas e incluso insectos, los cuales aparecerían frecuentemente en su obra posterior. Esto puede observarse, por ejemplo, en la ilustración de San Pedro Los viajes ocuparían gran parte de la vida de Escher a partir de ese momento. Hizo uno con dos amigos a Florencia en abril de 1922 y pasó todo el tiempo bosquejando y bebiendo. Escher después pasó otro mes más viajando solo por Italia, reuniendo material para usar en sus grabados experimentales en madera. Al inicio de su carrera como dibujante, Escher atacó solo brevemente el tema de "cubrir el plano"; desde una temprana edad había señales que apuntaban a ello. Muchos años después, una señora:

[...] recordó el cuidado con el que este pequeño niño [Escher] había seleccionado la forma, cantidad y tamaño de sus trozos de queso de tal manera que, puestos unos junto a otros, cubrieran de la manera más exacta posible la rebanada completa de pan. Este singular rasgo nunca lo abandonaría [...]

Su primera obra en la que presenta una división regular del plano se llama Ocho cabezas y fue terminada en 1922. Escher visitó España en junio de 1922, haciendo el viaje en un barco carguero y allí se revitalizó brevemente su interés en la división regular. Viajó a lo largo y ancho, visitó muchos palacios y lo inspiraron un gran número tanto de edificios como de paisajes. Un edificio que tendría una inmensa influencia en su vida fue el Palacio de la Alhambra de Granada.

Ocho cabezas El patio de los leones de la Alhambra Estanque en la Alhambra

Escher quedó anonadado ante la belleza del palacio morisco del siglo XIV y en especial por los azulejos decorativos que cubren muchas de las superficies del edificio. Al contrario que los árabes, Escher era entusiasta y se permitía usar objetos reconocibles en sus versiones ad-hoc de los azulejos. Hizo varios intentos de usar este estilo artístico durante los años siguientes pero estaba descontento tanto por el tiempo que le llevaba esta pasión (debido a su naturaleza de "ensayo y error") y por la baja calidad de su trabajo final así que dejó de lado la división regular durante varios años. Escribió, alrededor de 1924, que:

[...] por primera vez imprimí sobre una tela un motivo de un solo animal grabado en madera que se repite de acuerdo con cierto sistema, adhiriéndome al principio de que no queden espacios en blanco. Presenté esta tela junto con mis otras obras pero no tuve éxito con ella.

A su regreso de España, Escher se fue a vivir a Italia. De nuevo viajó ampliamente y en 1923, mientras estaba en la ciudad de Ravello, conoció a su futura esposa, Jetta Umiker. Se casaron el 12 de junio de 1924 y se quedaron a vivir en Frascati, a las afueras de Roma. Tendrían tres hijos: George (nacido el 23 de junio de 1926 en Frascati), Arturo (nacido el 8 de diciembre de 1928) y Jan (6 de marzo de 1938). Escher y su familia vacacionaron frecuentemente por Italia durante la siguiente década. Siguieron años de pintar el paisaje italiano, generalmente desde perspectivas imposibles, hasta que la familia fue forzada a abandonar Italia debido al alzamiento fascista que se desarrolló en Italia durante el verano de 1925. Se mudaron al pueblo montañés de Chateau-d'Oex en Suiza pero Jetta extrañaba Italia y los altos precios suizos forzaron a Escher a vender más grabados. Al principio la familia estaba infeliz en sus nuevos rumbos y, al faltarle la inspiración para su trabajo, Maurits y Jetta iniciaron una excursión al Mediterráneo. Escher consiguió negociar un trato con la compañía naviera Adria, que le dio pasaje y comidas gratis a él y también un pasaje de ida a Jetta. Hizo el pago con impresiones que completó usando bocetos que hizo durante el viaje. Éste empezó el 26 de abril de 1936 y durante los siguientes dos meses la pareja hizo volúmenes de bocetos con los cuales poder trabajar en el futuro. La fascinación de Escher con el orden y la simetría se apoderó de su vida después de este viaje al Mediterráneo en 1936, después de su segunda visita a la Alhambra. Escher señaló que ésta fue:

[...] la fuente más rica de inspiración de la que he bebido.

Escher y su esposa pasaron días enteros trabajando en el Palacio de la Alhambra donde hicieron tantos bocetos como pudieron, para deleite de los numerosos turistas que todos los días visitaban el lugar. Estos bocetos se convertirían en una fuente fundamente de mucho del trabajo posterior de Escher. Después de este viaje, Escher se obsesionó con el concepto de la división regular del plano. Escribió:

Sigue siendo una actividad extremadamente absorbente, una verdadera manía a la cual me he vuelto adicto y de la cual muchas veces me es difícil separarme.

Escher sentía que podía mejorar el trabajo de los artistas árabes y usó sus bocetos como una cuadrícula geométrica sobre la cual diseñar sus propios personajes para llenar el plano. Experimentó con muchos motivos distintos, tales como pájaros, levantadores de pesas y leones que aparecen en muchos de sus primeros diseños. Toda su obra durante este periodo se basaba fuertemente en su propia imaginación junto con sus bocetos españoles y le consumía gran cantidad de tiempo. En octubre de 1937 Escher mostró parte de su nuevo trabajo a su hermano Berend, quien para ese entonces era profesor de geología de la Universidad de Leiden, cuando ambos visitaban el hogar familiar en La Haya. Al reconocer la conexión entre los grabados de su hermano y la cristalografía, Berend envió a su hermano una lista de artículos que creía que podrían ayudarle. Este fue el primer contacto de Escher con las matemáticas. Escher leyó un artículo de Pólya de 1924 sobre simetría de grupos en el plano. Aunque no entendía el concepto abstracto de grupos discutido en el artículo, sí entendió los 17 grupos de simetría en el plano allí descritos. Subsecuentemente aprendió por sí mismo los principios bajo los cuales opera cada uno de los 17 grupos. Entre 1937 y 1941, Escher trabajó sobre los posibles embaldosados (o teselaciones) periódicos que producen 43 dibujos coloreados con una amplia variedad de tipos de simetría. Adoptó un acercamiento muy matemático con un estudio sistemático usando una notación que inventó él mismo. Escher también estudió un artículo escrito por F. Haag en 1923 y finalmente retó algunos de los puntos de vista expresados en la literatura después de investigar más sobre el tema. Hacia finales de 1937 la familia Escher se mudó a Bélgica, que se convertiría en su hogar hasta el 20 de febrero de 1941 cuando el ejército invasor alemán los obligó a huir hacia Baarn, en Holanda. La Segunda Guerra Mundial fue un periodo sumamente emotivo para Escher que le impidió concentrarse en su trabajo. Durante los años siguientes, Escher hizo numerosos grabados en madera utilizando cada uno de los 17 grupos de simetría. Con la práctica, sus habilidades mejoraron naturalmente y como resultado logró diseñar y completar cada pieza mucho más rápido que en años anteriores. Su arte formó parte integral de su vida familiar y Escher podía trabajar en su estudio entre las 8:00 y las 16:00 todos los días. Nuevos conceptos podían tardar meses o incluso años para cuajar antes de que la obra final fuera discutida y explicada a la familia. Uno de sus hijos escribió:

El final del ciclo, hacer la primera impresión, le daba a papá una mezcla de júbilo y tristeza. Era emocionante y satisfactorio levantar el papel por primera vez de la madera entintada, ver la xilografía terminada, nítida e inmaculada, aparecer gradualmente alrededor de la orilla del papel conforme era cuidadosamente levantado. Pero papá siempre tenía una sensación de decepción, de no haber podido dibujar adecuadamente sus pensamientos. Después de todo su esfuerzo, ¡qué lejos quedaba el resultado respecto a la idea originalmente tan lúcida y engañosamente simple!

La extensiva investigación culminó en 1941 con su primer cuaderno División regular del plano con polígonos asimétricos congruentes. Este cuaderno fue ampliado y mejorado durante el año siguiente, cuando se incluyeron los resultados obtenidos de sus extensas investigaciones sobre la división basada en el color. Estos libros no se hicieron para ser publicados sino como información de fondo que le permitiera continuar como un artista visionario. Los cuadernos son evidencia del hecho de que Escher se había convertido en un matemático investigador de primer orden, a pesar de sus sentimientos de inseguridad matemática. Había desarrollado su propio sistema de categorización, el cual cubría todas las posibles combinaciones de forma, color y propiedades simétricas. Como tal, había estudiado sin saberlo, áreas de la cristalografía años antes de que lo hiciera ningún matemático profesional que trabajara en ese campo. Escribió:

Hace mucho tiempo, me atreví a entrar en este ámbito [de la división regular del plano] en uno de mis deambulares... Sin embargo, al otro lado llegué a un área deshabitada... Llegué a la puerta abierta de las matemáticas. A veces pienso que he recorrido toda la zona [...] y después descubro repentinamente una nueva senda y experimento delicias que no había visto antes

A Escher lo inundaron las peticiones para dar conferencias por el mundo entero. En una de ellas, en 1953, Escher dijo: "Muchas veces me he sentido más cercano a quienes trabajan científicamente (aunque sin duda no lo hago yo) que a mis compañeros artistas". Hacia 1956 los intereses de Escher cambiaron de nuevo, llevando a la división regular del plano a un nivel más alto al representar el infinito sobre un plano bidimensional fijo. Al inicio de su carrera había usado el concepto de un lazo cerrado para tratar de expresar el infinito, como lo demuestra en Jinetes.

Jinetes

Había puesto sus diseños sobre diversos objetos tridimensionales tales como columnas y esferas en los años cuarenta, también como un intento de darle una perspectiva infinita a su obra. Más adelante trató de trabajar con el concepto de similitudes, utilizando motivos idénticos de tamaño descendiente, acomodados en series de círculos concéntricos pero, como sucedió con mucha de su obra, no quedó satisfecho con la calidad del producto final. En 1958 Escher conoció a Coxeter y se convirtieron en amigos de por vida. Escher encontró un artículo escrito por Coxeter y, aunque nuevamente no logró comprender el texto, pudo determinar las reglas de las teselaciones hiperbólicas usando nada más los diagramas del artículo. Escher agradeció a Coxeter enviándole una copia de una de sus nueva obras: Límite circular I. Escher continuó desarrollando y mejorando este campo y produjo muchas otras impresiones usando tanto círculos como cuadrados como marco para sus obras. Este estilo de obra de arte necesitaba enorme dedicación porque requiere una planeación cuidadosa y bocetos preliminares junto con la habilidad y la mano para grabar pero era una gran fuente de satisfacción para Escher.

Distintos límites circulares (LM):

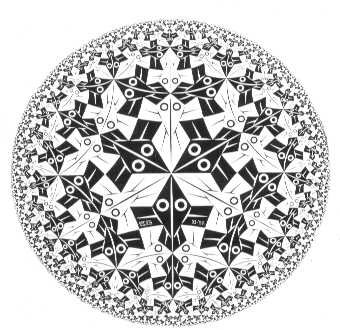
LM I LM III LM IV

Escribió:

Descubrí una vez más que la mano humana es capaz de ejecutar movimientos pequeños pero totalmente controlados siempre y cuando el ojo vea con suficiente claridad lo que hace la mano.

En 1995 Coxeter publicó un artículo en el que se demostraba que Escher había conseguido la perfección matemática en uno de sus grabados. Círculo límite III fue creado usando solamente instrumentos simples de dibujo y la gran intuición de Escher pero Coxeter probó que:

[...] [Escher] lo hizo milimétricamente bien, al milímetro absolutamente [...] Desafortunadamente no vivió lo suficiente para ver mi reivindicación matemática.

Esta demostración sirve para ensalzar la maravillosa habilidad natural de Escher para combinar tanto las aptitudes artísticas y técnicas que aprendió de otros para formar diseños matemáticamente perfectos. Para 1958 Escher había logrado una fama extraordinaria. Continuó dando conferencias y teniendo correspondencia con personas ansiosas de aprender de él. Hizo la primera exposición importante de su obra y apareció en la revista Time. Escher recibió numerosos premios durante su carrera, incluyendo el título de Caballero de Oranje Nassau (1955) y regularmente era comisionado para diseñar arte para dignatarios de todo el mundo. En 1958 publicó División regular del plano y en esta obra afirma que:

Al principio no tenía la menor idea de que fuera posible construir sistemáticamente mis figuras. No sabía [...] que esto era posible para alguien sin entrenamiento matemático y, especialmente, como resultado de desarrollar mi propia teoría inexperta, lo que me forzó a pensar con cuidado en las posibilidades.

Nuevamente en División regular del plano Escher escribe:

En los ámbitos matemáticos, la división regular del plano ha sido considerada teóricamente [...] [Los matemáticos] han abierto la puerta que lleva a un extenso dominio pero no han incursionado en él ellos mismos. Por su misma naturaleza, están más interesados en la manera en que se abre la puerta que en el jardín que yace tras ella.

La obra de Escher cubrió gran variedad de temas a lo largo de su vida. Su temprano amor por los retratos, por los paisajes romanos e italianos y por la naturaleza, finalmente dieron paso a la división regular del plano. Muchas de sus piezas fueron dibujadas desde perspectivas inusuales creando así enigmáticos efectos espaciales. Era hábil en el arte de muchas técnicas de impresión distintas, tales como la xilografía, litografía y la media tinta. Más de 150 obras coloridas y bien reconocibles dan testimonio del ingenio de Escher y de su interés por la división regular del plano. Logró capturar la noción de espacio hiperbólico en un plano bidimensional fijo y también trasladar los principios de la división regular a muchos objetos tridimensionales como esferas, columnas y cubos. Varias de sus impresiones combinan imágenes bi y tridimensionales con efectos asombrosos como se demuestra, por ejemplo, en Reptiles. Escher escribió:

Cuando un elemento de la división del plano me sugiere la forma de un animal, inmediatamente pienso en un volumen. La "forma plana" me irrita - siento como si yo estuviera gritándole a mis figuras: ¡Son ustedes demasiado ficticias para mí; se quedan ahí estáticas y congeladas juntas; hagan algo, salgan de allí y muéstrenme de lo que son capaces!. Así que hago que salgan del plano. Pero ¿en realidad lo hacen? Al contrario, soy deliberadamente inconsistente, sugiriendo la plasticidad del plano mediante luces y sombras.

Le fascinaba la topología, la cual empezó a estudiarse apenas durante su vida, como lo ilustra en la cinta de Möbius. Hacia el final de su vida aprendió mucho del matemático británico Roger Penrose y usó este conocimiento para diseñar muchos grabados "imposibles" tales como Catarata o Subida y bajada. Escher usó imágenes para narrar una historia en su serie de dibujos Metamorfosis. Estos diseños reúnen muchas de las habilidades de Escher y muestran la transformación de un objeto bien definido en otro mediante una serie de pequeños cambios en un patron regular sobre el plano. Metamorfosis I en particular, impresa en 1933, da una visión del cambió de estilo artístico que tuvo lugar en la vida de Escher en ese momento. Una línea de costa italiana se transforma mediante una serie de polígonos convexos en un patrón regular en el plano hasta llegar finalmente a un motivo humano bien definido y colorido, expresando su cambio de perspectiva del paisajismo a la división regular del plano.

La Catarata Subida y Bajada

Escher cayó enfermo inicialmente en 1964 mientras daba una serie de conferencias en Norteamérica. Como resultado, se vio forzado a reducir su itinerario significativamente, dedicando la mayor parte de su tiempo después a la correspondencia con amigos. En ella se describen su últimos años de la siguiente manera:

Cuando la visión del mundo de Escher se volvió hacia adentro, fue cuando produjo sus intrigantes impresiones más conocidas -las cuales, dejando el arte de lado- eran de verdad intelectualmente juguetonas, aunque él no lo era. Su vida se volcó hacia adentro, se recluyó y tuvo pocos amigos. [...] Murió después de una prolongada enfermedad...

Le tomó seis meses completar su última obra gráfica, la xilografía Serpientes, y fue finalmente desvelada en julio de 1969. Este excepcional grabado enfila hacia el infinito tanto en el centro como en las orillas del dibujo. Después de más operaciones, Escher se mudó al hogar Rosa Spier en Laren y poco después murió en el hospital.

[Todas las obras de M. C. Escher © 2001 Cordon Art-Baarn-Holanda. Todos los derechos reservados. Usadas con permiso por la página original.] Artículo de: J J O'Connor y E F Robertson basado en un proyecto de Malcolm Raven.

MacTutor History of Mathematics Archive Bibliografía

Biografía en Encyclopaedia Britannica.
F H Bool et al., M C Escher, His Life and Complete Graphic Work (New York, 1982).
H S M Coxeter, M Emmer, R Penrose and M L Teuber, M C Escher : Art and Science (Amsterdam, 1987).
D Hofstadter, Godel, Escher, Bach: An eternal Golden Braid (New York, 1979).
C H MacGillvary, Symmetry aspects of M C Eschers Periodic drawings (1965).
D Schattschneider, Visions of Symmetry (New York, 1990).
S Strauss, M C Escher (The Globe and Mail, 9 May 2024).
D Schattschneider, Escher: A mathematician in spite of himself, in R K Guy and R E Woodrow (eds), The Lighter Side of Mathematics (Washington, 1994), 91-100.
D Schattschneider, Escher: A mathematician in spite of himself, Structural Topology 15 (1988), 9-22.